Bag of Tokens Solution In C++/Java/Python/JS
Problem Description
You start with an initial power of power, an initial score of 0, and a bag of tokens given as an integer array tokens, where each tokens[i] denotes the value of tokeni.
Your goal is to maximize the total score by strategically playing these tokens. In one move, you can play an unplayed token in one of the two ways (but not both for the same token):
-Face-up: If your current power is at least tokens[i], you may play tokeni, losing tokens[i] power and gaining 1 score.
-Face-down: If your current score is at least 1, you may play tokeni, gaining tokens[i] power and losing 1 score.
Return the maximum possible score you can achieve after playing any number of tokens.
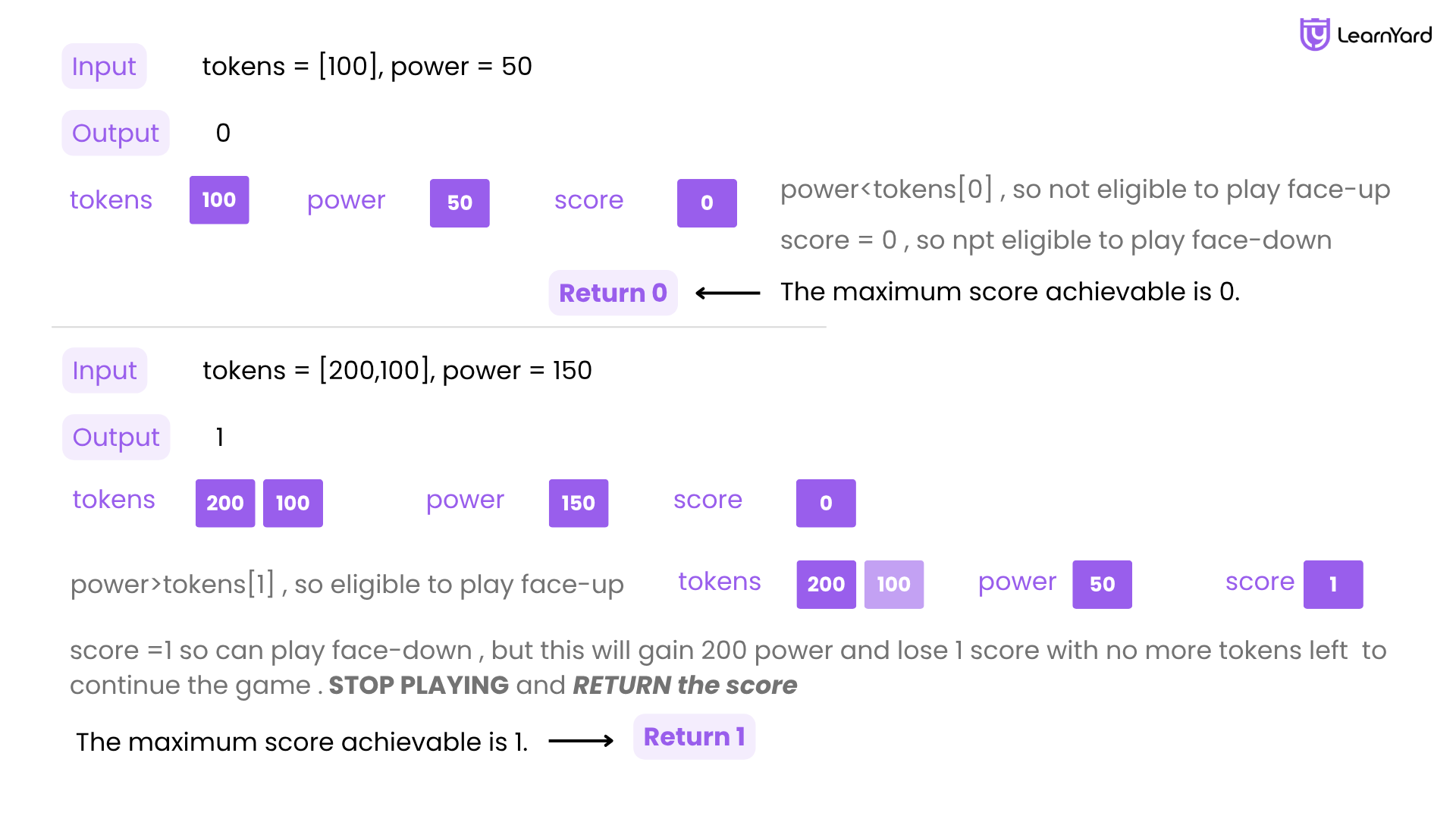
Examples
Input: tokens = [100], power = 50
Output: 0
Explanation: Since your score is 0 initially, you cannot play the token face-down. You also cannot play it face-up since your power (50) is less than tokens[0] (100).
Input: tokens = [200,100], power = 150
Output: 1
Explanation: Play token1 (100) face-up, reducing your power to 50 and increasing your score to 1.There is no need to play token 0, since you cannot play it face-up to add to your score. The maximum score achievable is 1.
Constraints
- 0 <= tokens.length <= 1000
- 0 <= tokens[i], power < 104
The first thing we wonder is: how can we play tokens in a way that gives the highest score using the power we have? A basic idea is to try every possible play—face-up to gain score or face-down to regain power. This brute-force way is slow but helps us understand how each move affects the game. Once that’s clear, we shift to a greedy method: use the smallest tokens to earn score and the largest ones to refill power when stuck.
Brute Force Approach
Intuition
Since we want to get the highest score from the tokens, the first idea that comes to mind is to try out all the different ways we can play them. For each token, we have two options: play it face-up to gain a score (but lose power), or play it face-down to gain power (but lose a score). So we try every possible sequence of these moves to see which one gives the best result.
Why Try Every Possible Way of Playing Tokens?
Each move affects our power and score, and once a token is used, we can’t use it again. So the order in which we play them really matters.
Let’s say:
tokens = [200, 100], power = 150
We might first try token 100 face-up (since we have enough power), then see what to do next.
But maybe trying token 200 first gives a better path? Or maybe skipping one is better?
Since we don’t know which path is best, trying all combinations ensures we don’t miss the optimal one.
For this, we can use a recursive function that keeps track of current power, score, and which tokens have been used. At each step, we try both face-up and face-down moves (if possible), and recursively continue. We also keep track of the maximum score we’ve seen along the way and return that at the end.
Approach
Step 1: Sort the Token Array (Optional for Consistency)
Although sorting isn't strictly necessary for brute-force logic, we perform it to ensure a consistent order of token access. This helps make the recursion behavior predictable and helps in tracing or debugging.
Sorting also allows you to start with the smallest token first and helps with power comparisons more logically in face-up and face-down decisions.
Step 2: Create a Recursive DFS Function
We define a recursive function dfs that tries all possibilities:
- Either play a token face-up if we have enough power
- Or play it face-down if we have at least 1 score
This recursive method explores every valid combination of token usage, and at each step, it checks if a better score is achieved.
Step 3: Track Which Tokens Are Already Used
Since each token can be played only once, we maintain a used array (or list) of booleans to mark which tokens are already played in the current recursive path.
Before trying any token, we check if it's already been used.
Step 4: Make Choices at Each Token
For every unused token:
- If the current power is greater than or equal to the token’s value, we can play it face-up (gain 1 score, lose power)
- If the current score is at least 1, we can play it face-down (gain power, lose 1 score)
After each choice, we:
- Mark the token as used
- Make a recursive call to try further moves
- Then backtrack by unmarking the token
Step 5: Track the Maximum Score
Each time we enter the dfs function, we update a global or class-level variable maxScore with the maximum value of score seen so far.
This ensures that even if a better score appears in a deeper recursive branch, we capture it.
Step 6: Return the Final maxScore
After exploring all possible combinations of token plays through recursion, we return maxScore as the final result.
This value represents the best possible score achievable by playing tokens in any order using brute-force.
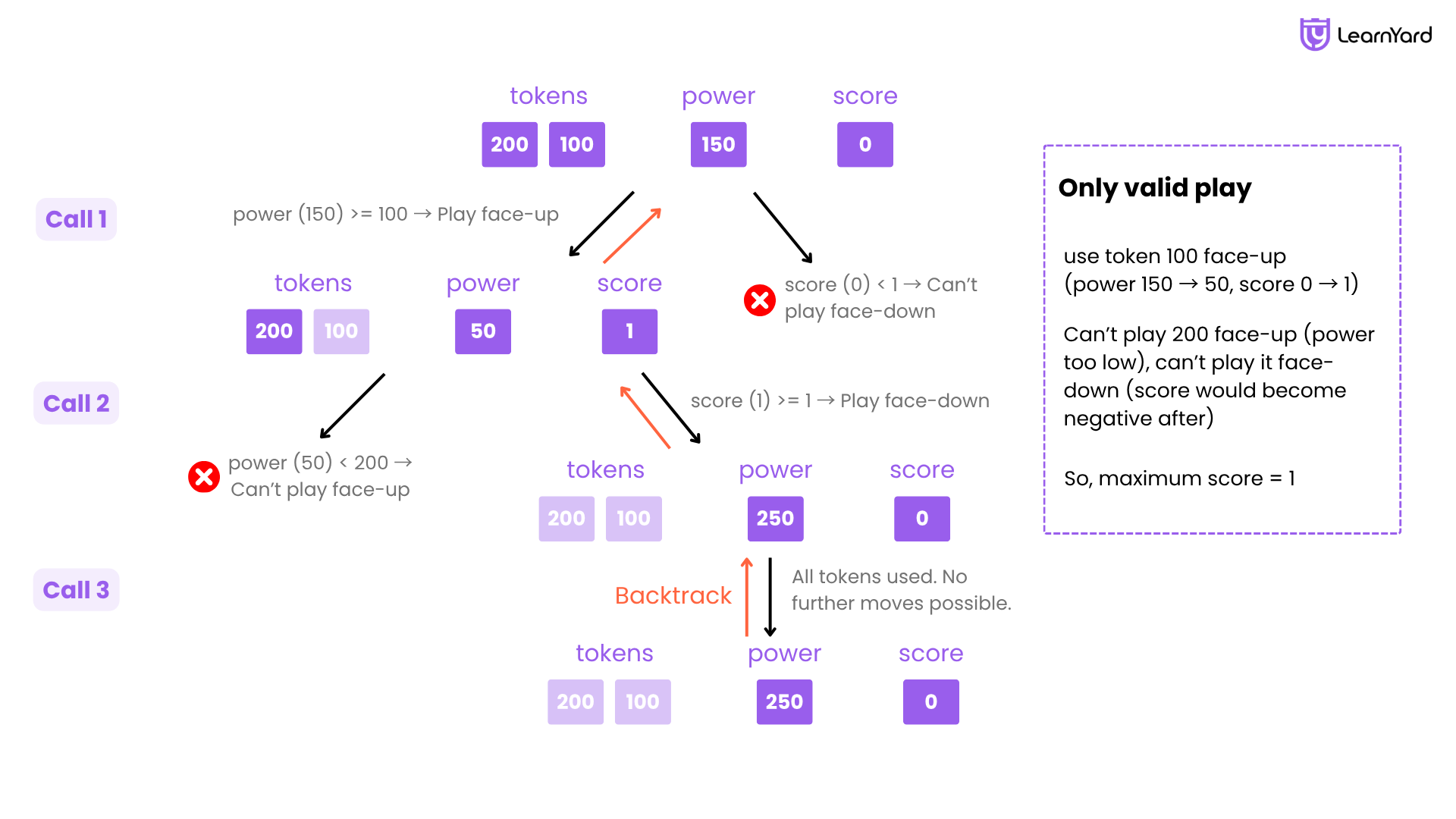
Dry Run
Input: tokens = [200, 100], power = 150
Initial score = 0
All tokens are unused: [False, False]
We will try every possible sequence of playing the tokens.
Call 1:
- power = 150, score = 0, used = [False, False], maxScore = 0
Loop over tokens:
Try i = 0 → token = 200
- power (150) < 200 → Can’t play face-up
- score (0) < 1 → Can’t play face-down
→ Skip this token.
Try i = 1 → token = 100
- power (150) >= 100 → Play face-up
→ power = 150 - 100 = 50
→ score = 0 + 1 = 1
→ mark used[1] = True
→ Recurse with:
- power = 50, score = 1, used = [False, True]
Call 2:
- power = 50, score = 1, used = [False, True], maxScore = 1
Loop over tokens:
Try i = 0 → token = 200
- power (50) < 200 → Can’t play face-up
- score (1) >= 1 → Play face-down
→ power = 50 + 200 = 250
→ score = 1 - 1 = 0
→ mark used[0] = True
→ Recurse with:
- power = 250, score = 0, used = [True, True]
Call 3:
- power = 250, score = 0, used = [True, True], maxScore = 1
- All tokens used. No further moves possible.
- Backtrack.
Backtrack to Call 2:
- Undo used[0] → used = [False, True]
- Done with all tokens.
Backtrack to Call 1:
- Undo used[1] → used = [False, False]
- Done trying all tokens.
Final Output : 3
- Only valid play: use token
100face-up (power 150 → 50, score 0 → 1) - Can’t play 200 face-up (power too low), can’t play it face-down (score would become negative after)
- So, maximum score = 1
Code for All Languages
C++
#include <iostream> // For cin and cout
#include <vector> // For using vector container
#include <algorithm> // For sort and max functions
using namespace std;
class Solution {
public:
int maxScore = 0; // To track the maximum score achieved during recursion
// Recursive helper function to try all token play possibilities
void dfs(vector<int>& tokens, vector<bool>& used, int power, int score) {
// Step 1: Update maxScore if current score is higher
maxScore = max(maxScore, score);
// Step 2: Try each unused token
for (int i = 0; i < tokens.size(); i++) {
if (!used[i]) {
// Step 3: Option 1 – Play token face-up if enough power
if (power >= tokens[i]) {
used[i] = true;
dfs(tokens, used, power - tokens[i], score + 1);
used[i] = false; // Backtrack
}
// Step 4: Option 2 – Play token face-down if score is at least 1
else if (score >= 1) {
used[i] = true;
dfs(tokens, used, power + tokens[i], score - 1);
used[i] = false; // Backtrack
}
}
}
}
int bagOfTokensScore(vector<int>& tokens, int power) {
// Step 1: Sort tokens (optional, helps for consistent order)
sort(tokens.begin(), tokens.end());
// Step 2: Create a used array to track token usage
vector<bool> used(tokens.size(), false);
// Step 3: Start DFS from initial state
dfs(tokens, used, power, 0);
// Step 4: Return the maximum score found
return maxScore;
}
};
int main() {
int n, power;
// Input number of tokens
cin >> n;
vector<int> tokens(n);
// Input token values
for (int i = 0; i < n; i++) {
cin >> tokens[i];
}
// Input initial power
cin >> power;
Solution sol;
int result = sol.bagOfTokensScore(tokens, power);
// Output the maximum score achievable
cout << result << endl;
return 0;
}Java
import java.util.*; // For Scanner, Arrays, and List
class Solution {
private int maxScore = 0; // To keep track of highest score found
// Recursive helper function to explore all play combinations
private void dfs(int[] tokens, boolean[] used, int power, int score) {
// Step 1: Update maxScore if current score is higher
maxScore = Math.max(maxScore, score);
// Step 2: Try every unused token
for (int i = 0; i < tokens.length; i++) {
if (!used[i]) {
// Step 3: Option to play face-up if enough power
if (power >= tokens[i]) {
used[i] = true;
dfs(tokens, used, power - tokens[i], score + 1);
used[i] = false; // Backtrack
}
// Step 4: Option to play face-down if score available
else if (score >= 1) {
used[i] = true;
dfs(tokens, used, power + tokens[i], score - 1);
used[i] = false; // Backtrack
}
}
}
}
public int bagOfTokensScore(int[] tokens, int power) {
// Step 1: Sort tokens (optional for consistent behavior)
Arrays.sort(tokens);
// Step 2: Create used array to track which tokens are played
boolean[] used = new boolean[tokens.length];
// Step 3: Start DFS recursion
dfs(tokens, used, power, 0);
// Step 4: Return the highest score achieved
return maxScore;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input the number of tokens
int n = sc.nextInt();
int[] tokens = new int[n];
// Input the token values
for (int i = 0; i < n; i++) {
tokens[i] = sc.nextInt();
}
// Input the initial power
int power = sc.nextInt();
Solution sol = new Solution();
int result = sol.bagOfTokensScore(tokens, power);
// Output the result
System.out.println(result);
}
}
Python
from typing import List # For specifying the input/output types
class Solution:
def __init__(self):
self.max_score = 0 # To track the highest score found
# Recursive DFS function to try all token plays
def dfs(self, tokens: List[int], used: List[bool], power: int, score: int):
# Step 1: Update the max_score at each step
self.max_score = max(self.max_score, score)
# Step 2: Try every unused token
for i in range(len(tokens)):
if not used[i]:
# Step 3: Option to play face-up if power is enough
if power >= tokens[i]:
used[i] = True
self.dfs(tokens, used, power - tokens[i], score + 1)
used[i] = False # Backtrack
# Step 4: Option to play face-down if score is at least 1
elif score >= 1:
used[i] = True
self.dfs(tokens, used, power + tokens[i], score - 1)
used[i] = False # Backtrack
def bagOfTokensScore(self, tokens: List[int], power: int) -> int:
# Step 1: Sort the tokens (optional for consistent traversal)
tokens.sort()
# Step 2: Initialize the used array for DFS
used = [False] * len(tokens)
# Step 3: Start DFS from initial state
self.dfs(tokens, used, power, 0)
# Step 4: Return the maximum score achieved
return self.max_score
# Driver Code
if __name__ == "__main__":
n = int(input()) # Input the number of tokens
tokens = list(map(int, input().split())) # Input token values
power = int(input()) # Input initial power
sol = Solution()
result = sol.bagOfTokensScore(tokens, power)
# Output the maximum score
print(result)
Javascript
/**
* @param {number[]} tokens - The array of token values
* @param {number} power - The initial power available
* @return {number} - The maximum score that can be achieved
*/
var bagOfTokensScore = function(tokens, power) {
// Step 1: Sort tokens to help with consistent order
tokens.sort((a, b) => a - b);
let maxScore = 0;
// Step 2: DFS helper function to try all combinations
const dfs = (used, power, score) => {
maxScore = Math.max(maxScore, score);
// Step 3: Try each token
for (let i = 0; i < tokens.length; i++) {
if (!used[i]) {
// Step 4: Try face-up if possible
if (power >= tokens[i]) {
used[i] = true;
dfs(used, power - tokens[i], score + 1);
used[i] = false; // Backtrack
}
// Step 5: Try face-down if possible
else if (score >= 1) {
used[i] = true;
dfs(used, power + tokens[i], score - 1);
used[i] = false; // Backtrack
}
}
}
};
// Step 6: Initialize used array and start DFS
const used = new Array(tokens.length).fill(false);
dfs(used, power, 0);
// Step 7: Return the highest score found
return maxScore;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
rl.on("line", function(line) {
inputs.push(line.trim());
// Read tokens and power input
if (inputs.length === 2) {
const tokens = inputs[0].split(' ').map(Number);
const power = parseInt(inputs[1]);
const result = bagOfTokensScore(tokens, power);
console.log(result);
rl.close();
}
});
Time Complexity: O(2ⁿ)
Exploring All Possibilities: O(2ⁿ)
We try every possible sequence of moves — face-up, face-down, or skip — for each token.
For every token, we have two main choices:
- Play it face-up (if power allows)
- Play it face-down (if score allows)
Let’s denote:
n = number of tokens
So, in the worst case, we explore 2 choices per token → total of 2ⁿ possible paths to simulate.
Each Recursive Path: O(n)
Along each path, we keep a visited array or a set to track used tokens, and check conditions like current power and score.
These operations (checking and updating state) take up to O(n) time in total.
Final Time Complexity: O(n × 2ⁿ)
Since we explore up to 2ⁿ paths and each path can involve up to n work, the total time complexity is:O(n × 2ⁿ)
This is exponential, which makes the brute-force approach only suitable for small input sizes (e.g., n ≤ 15).
Space Complexity: O(n)
Auxiliary Space Complexity: O(n)
In the brute-force approach, we use additional memory to keep track of:
- A used[] array or visited set of size n to remember which tokens have already been played
- Function call stack due to recursion — in the worst case, recursion can go as deep as n levels (one level per token)
- Temporary variables like current power, score, and maxScore passed during recursion
The used[] array is the main contributor to extra space.
So, the auxiliary space used is O(n)
Total Space Complexity: O(n)
This includes:
- Input space: The input array tokens of length n → O(n)
- Auxiliary space: The used[] array and recursive stack → O(n)
No large data structures like output lists or matrices are used — only an integer maxScore is returned.
Final total space complexity = O(n)
Why the Brute-Force Approach Leads to TLE
e main reason this brute-force approach is slow and causes a Time Limit Exceeded (TLE) error is due to its exponential time complexity and the size of the input.
In the worst case, the number of tokens n can be up to 1000.
In this approach:
- We try every possible way of playing tokens — either face-up or face-down — which leads to 2ⁿ possible paths to explore.
- For example, even with just 20 tokens, that results in over 1 million (2²⁰ ≈ 1,048,576) recursive paths.
- With 25–30 tokens, it becomes hundreds of millions to billions of operations.
Even though each step just checks power, score, and marks a token as used, doing so millions or billions of times far exceeds time limits.
Most coding platforms (like LeetCode) allow around 10⁷ operations per second, and this brute-force approach can easily blow past that in larger inputs.
So while this method is correct, it’s not practical for large inputs and will almost always fail on performance due to its O(2ⁿ) time behavior.
So now, we’re thinking smarter: instead of trying every possible move combination and wasting time exploring paths that don’t even help, we switch to a greedy approach that makes the best move at each step. By sorting the tokens and always spending the smallest one for score or selling the biggest one for power, we avoid unnecessary backtracking and make progress efficiently. It’s like moving from blind guessing to a strategy that picks the most valuable action in real-time — faster, smarter, and perfect for scaling to large input sizes.
Optimal Approach
Intuition
After realizing that the brute-force way is too slow, the next idea is to make moves that give us the most value with the least cost. That’s where the greedy mindset comes in.
We want to maximize score, and to do that, we must spend power by playing tokens face-up. But we don’t want to waste power. So instead of picking tokens randomly, we choose the cheapest token (the one with the smallest value). That way, we lose the least amount of power for every score we gain — that’s maximum value for minimum cost.
Now let’s say we run into a situation where we don’t have enough power left to play any more tokens face-up. But if we already have at least 1 score, we’re allowed to play a token face-down. This gives us back some power — but costs 1 score. So here, we use the largest available token, because it gives us the biggest power boost in one move.
By repeating this logic — spend the smallest token for score, reclaim power using the biggest token when stuck — we’re always making the smartest move possible at each step. That’s what makes this approach greedy: we’re not looking ahead to all options like brute force does, we’re just making the best immediate decision every time.
Why Smallest for Score and Largest for Power?
Because playing a small token face-up costs less and gives us 1 score — it's the most efficient way to increase our score.
On the other hand, if we're stuck (no power left), we don't want to sell a small token back — that gives little power. Instead, we trade the largest unused token to gain the most power possible with just 1 score.
Example:
tokens = [100, 200, 300, 400], power = 200
→ Use 100 face-up → power = 100, score = 1
→ Use 400 face-down → power = 500, score = 0
→ Use 200 face-up → power = 300, score = 1
→ Use 300 face-up → power = 0, score = 2
This way we alternate between gaining score and refilling power, but always in the most optimal order.
To do this, we sort the tokens in increasing order and then use a two-pointer technique to process the tokens from both ends. One pointer, called left, starts at the beginning of the array and always points to the smallest unused token. The other pointer, right, starts at the end of the array and always points to the largest unused token. The idea is simple: if we have enough power to play the smallest token, we use it face-up to gain 1 score and move left forward. But if we don’t have enough power and already have at least 1 score, we play the largest unused token face-down to regain power and move right backward. This way, left helps us increase score using the cheapest tokens, and right helps us regain power using the most valuable tokens. Both pointers keep pushing toward each other, and we stop once they cross or we can’t make any more valid moves.
Approach
Step 1: Sort the Tokens in Ascending Order
We begin by sorting the tokens array in increasing order.
- This lets us access the cheapest token (smallest value) when trying to gain score by playing it face-up.
- It also lets us access the most expensive token (largest value) when trying to regain power by playing it face-down.
Sorting allows us to make the most efficient greedy choices.
Step 2: Initialize Two Pointers and Score Trackers
We use two pointers:
- left starts from the beginning of the array and moves right.
- right starts from the end of the array and moves left.
We also initialize:
- score to track the current score
- maxScore to track the maximum score reached so far
This setup allows us to simulate both actions — gaining score or recovering power — depending on the current state.
Step 3: Play Tokens While Possible
We run a loop while left <= right, which means there are still unplayed tokens.
Inside the loop:
- If power >= tokens[left], we play the token face-up:
- Subtract its value from power
- Add 1 to score
- Move left forward
- Update maxScore if score is greater than previous maximum
- Else if score >= 1, we play the token face-down:
- Add its value to power
- Subtract 1 from score
- Move right backward
This logic ensures we always:
- Gain score when we have enough power
- Gain power when we’re stuck but have some score to spare
Step 4: Stop When No More Valid Moves
If we can’t do either action (not enough power and not enough score), the loop ends.
At this point, we’ve tried the best possible strategy using greedy decisions.
Step 5: Return the Maximum Score
After the loop finishes, we return maxScore, which holds the highest score we could reach during any stage of the game.
This value is the final answer — the optimal score we can get using the most efficient greedy approach.
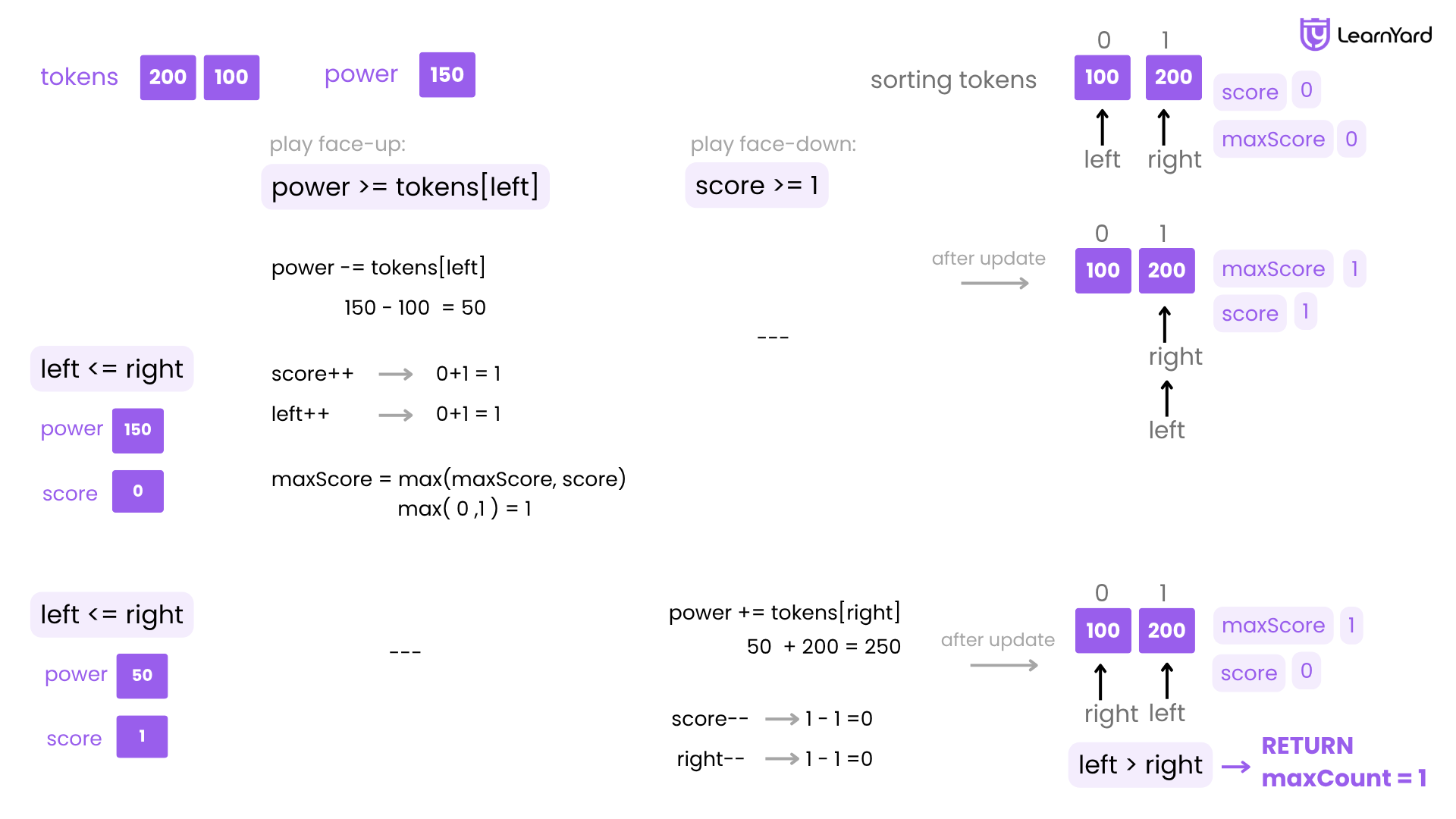
Dry Run
Let’s do a step-by-step dry run of the greedy two-pointer approach for the input:
input : tokens = [200, 100] , power = 150
We want to find the maximum score we can achieve by playing tokens face-up (gain score, lose power) or face-down (gain power, lose score).
Step 1: Sort Tokens
Original tokens = [200, 100]
After sorting → tokens = [100, 200]
This allows us to:
- Use the cheapest token for face-up play (100)
- Use the most expensive token for power gain if needed (200)
Step 2: Initialize Pointers and Score
We set up:
- left = 0
- right = 1 (last index)
- score = 0
- maxScore = 0
Step 3: Iteration-wise Dry Run
First Iteration
power = 150, score = 0, tokens[left] = 100
power >= tokens[left] → play face-up:
- power = 150 - 100 = 50
- score = 0 + 1 = 1
- left = 0 → 1
- maxScore = 1
Second Iteration
power = 50, score = 1, tokens[left] = 200
power < 200 → can't play face-up
score >= 1 → play face-down:
- power = 50 + 200 = 250
- score = 1 - 1 = 0
- right = 1 → 0
Third Iteration
left = 1, right = 0 → loop stops (left > right)
No more tokens left to play.
Final Output:
We only gained 1 score total. Even though we regained power by playing 200 face-down, we had no tokens left to play face-up with that extra power.
Maximum Score Achieved = 1
Code for All Languages
C++
#include <iostream> // For input and output using cin and cout
#include <vector> // For using the vector container
#include <algorithm> // For sort and max functions
using namespace std;
class Solution {
public:
int bagOfTokensScore(vector<int>& tokens, int power) {
// Step 1: Sort the tokens in ascending order
sort(tokens.begin(), tokens.end());
int score = 0;
int maxScore = 0;
// Step 2: Initialize two pointers for the leftmost and rightmost tokens
int left = 0;
int right = tokens.size() - 1;
// Step 3: Use a loop to play tokens as long as moves are possible
while (left <= right) {
if (power >= tokens[left]) {
// Step 4: Play token face-up (gain 1 score, lose power)
power -= tokens[left];
score++;
left++;
maxScore = max(maxScore, score); // Track max score reached
} else if (score >= 1) {
// Step 5: Play token face-down (gain power, lose 1 score)
power += tokens[right];
score--;
right--;
} else {
// Step 6: Break if neither move is possible
break;
}
}
// Step 7: Return the maximum score achieved
return maxScore;
}
};
int main() {
int n, power;
// Input the number of tokens
cin >> n;
vector<int> tokens(n);
// Input the token values
for (int i = 0; i < n; i++) {
cin >> tokens[i];
}
// Input the initial power
cin >> power;
Solution sol;
int result = sol.bagOfTokensScore(tokens, power);
// Output the result (maximum score achievable)
cout << result ;
return 0;
}
Java
import java.util.*; // For Scanner, Arrays, and List
class Solution {
public int bagOfTokensScore(int[] tokens, int power) {
// Step 1: Sort the tokens to access smallest and largest easily
Arrays.sort(tokens);
int left = 0;
int right = tokens.length - 1;
int score = 0;
int maxScore = 0;
// Step 2: Use two-pointer approach to maximize score
while (left <= right) {
if (power >= tokens[left]) {
// Step 3: Play token face-up (gain score, lose power)
power -= tokens[left];
score++;
left++;
maxScore = Math.max(maxScore, score);
} else if (score >= 1) {
// Step 4: Play token face-down (gain power, lose score)
power += tokens[right];
score--;
right--;
} else {
// Step 5: No more moves possible
break;
}
}
// Step 6: Return the maximum score achieved
return maxScore;
}
}
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input the number of tokens
int n = sc.nextInt();
int[] tokens = new int[n];
// Input the token values
for (int i = 0; i < n; i++) {
tokens[i] = sc.nextInt();
}
// Input the initial power value
int power = sc.nextInt();
Solution sol = new Solution();
int result = sol.bagOfTokensScore(tokens, power);
// Output the maximum score achievable
System.out.println(result);
}
}
Python
from typing import List # For specifying the input/output types
class Solution:
def bagOfTokensScore(self, tokens: List[int], power: int) -> int:
# Step 1: Sort the tokens to use smallest for score and largest for power recovery
tokens.sort()
left = 0
right = len(tokens) - 1
score = 0
max_score = 0
# Step 2: Use a loop to simulate greedy face-up and face-down moves
while left <= right:
if power >= tokens[left]:
# Step 3: Play token face-up (gain score, lose power)
power -= tokens[left]
score += 1
left += 1
max_score = max(max_score, score)
elif score >= 1:
# Step 4: Play token face-down (gain power, lose score)
power += tokens[right]
score -= 1
right -= 1
else:
# Step 5: Exit if no moves possible
break
# Step 6: Return the maximum score achieved
return max_score
# Driver Code
if __name__ == "__main__":
n = int(input()) # Input the number of tokens
tokens = list(map(int, input().split())) # Input token values
power = int(input()) # Input initial power
sol = Solution()
result = sol.bagOfTokensScore(tokens, power)
# Output the maximum score achievable
print(result)
Javascript
/**
* @param {number[]} tokens - The array of token values
* @param {number} power - The initial power available
* @return {number} - The maximum score that can be achieved
*/
var bagOfTokensScore = function(tokens, power) {
// Step 1: Sort tokens to access smallest and largest easily
tokens.sort((a, b) => a - b);
let left = 0;
let right = tokens.length - 1;
let score = 0;
let maxScore = 0;
// Step 2: Use two-pointer strategy to maximize score
while (left <= right) {
if (power >= tokens[left]) {
// Step 3: Play token face-up (gain score, lose power)
power -= tokens[left];
score++;
left++;
maxScore = Math.max(maxScore, score);
} else if (score >= 1) {
// Step 4: Play token face-down (gain power, lose score)
power += tokens[right];
score--;
right--;
} else {
// Step 5: No valid moves left
break;
}
}
// Step 6: Return the maximum score achieved
return maxScore;
};
// Driver code
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
let inputs = [];
rl.on("line", function(line) {
inputs.push(line.trim());
// Read tokens and power input
if (inputs.length === 2) {
const tokens = inputs[0].split(' ').map(Number);
const power = parseInt(inputs[1]);
const result = bagOfTokensScore(tokens, power);
console.log(result);
rl.close();
}
});
Time Complexity : O(n log n)
Sorting the Tokens — O(n log n)
We begin by sorting the tokens array so that we can always pick the smallest and largest tokens efficiently using two pointers.
Let’s denote:
- n = number of tokens
The sorting step takes O(n log n) time using a standard built-in sorting algorithm.
Two-Pointer Greedy Traversal — O(n)
After sorting, we use two pointers:
- left starts from the beginning of the array
- right starts from the end of the array
In each iteration, we either move left forward (when playing a token face-up) or move right backward (when playing one face-down).
Each token is used at most once, so the loop runs at most n times, which contributes O(n) time overall.
Final Time Complexity: O(n log n)
- Sorting step → O(n log n)
- Two-pointer loop → O(n)
- Work per iteration → O(1)
Since the sorting step dominates, the total time complexity is:O(n log n)
Space Complexity: O(1)
Auxiliary Space Complexity: O(1)
This refers to the extra memory used by the algorithm beyond the input and output.
In this greedy two-pointer approach, we use only a few integer variables:
- Two pointers: left and right
- A score counter and a maxScore tracker
All of these occupy constant space regardless of the input size.
We do not use any extra arrays, maps, or data structures that grow with the input.
Total Space Complexity: O(1)
This includes:
Input Space:
- The input array tokens is used directly and sorted in place → no extra space is created
Output Space:
- The result is a single integer (maximum score) → O(1)
Auxiliary Space:
- Just a few counters and pointers → O(1)
So, the total space used by the algorithm remains constant.
Final Space Complexity = O(1)
Learning Tip
Now we have successfully tackled this problem, let’s try these similar problems.
There are n children standing in a line. Each child is assigned a rating value given in the integer array ratings.You are giving candies to these children subjected to the following requirements:Each child must have at least one candy.Children with a higher rating get more candies than their neighbors.Return the minimum number of candies you need to have to distribute the candies to the children.