Advantage Shuffle Solution In C++/Java/Python/JS
Problem Description
You are given two integer arrays nums1 and nums2 both of the same length. The advantage of nums1 with respect to nums2 is the number of indices i for which nums1[i] > nums2[i].
Return any permutation of nums1 that maximizes its advantage with respect to nums2.
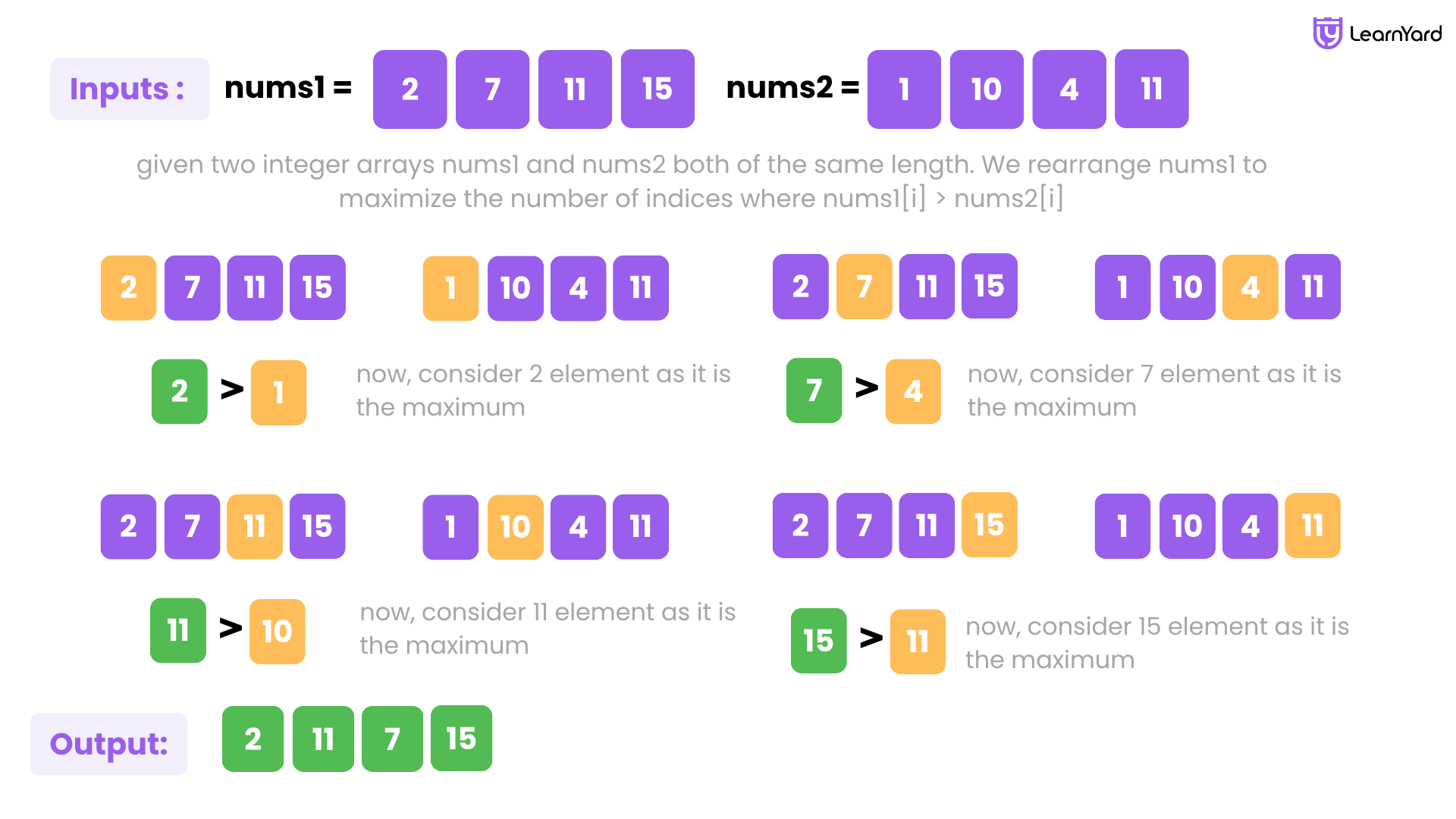
Example
Input: nums1 = [2,7,11,15], nums2 = [1,10,4,11]
Output: [2,11,7,15]
Explanation: We rearrange nums1 to maximize the number of indices where nums1[i] > nums2[i], such as 2 > 1, 11 > 10, 7 > 4, and 15 > 11.
Input: nums1 = [12,24,8,32], nums2 = [13,25,32,11]
Output: [24,32,8,12]
Explanation: We rearrange nums1 to maximize advantage, achieving 24 > 13, 32 > 25, and 12 > 11, while 8 remains unmatched.
Constraints
- 1 <= nums1.length <= 105
- nums2.length == nums1.length
- 0 <= nums1[i], nums2[i] <= 109
Figuring out "Advantage Shuffle" can be solved using different approaches. We will first figure out the most intuitive approach and move to the optimal approach if exists. Let's sit with a pen and paper and figure out the algorithm !!
Optimal Approach
Intuition
Imagine we have two arrays of the same length. Let's say:
nums1 = [3, 6, 7, 5]
nums2 = [2, 8, 4, 10]
Our goal is to rearrange nums1 such that we maximize the number of indices where nums1[i] > nums2[i]. How would we start thinking about this problem?
A good approach would be to try to match larger numbers from nums1 with smaller numbers in nums2.
That’s an interesting thought! Let’s break it down further. If we had full control, how would we assign numbers?
It would be best to ensure that each number in nums1 is greater than the corresponding number in nums2 whenever possible.
Right! But what if nums1 had a number that is smaller than every remaining number in nums2? What should we do?
Then there would be no choice but to put it somewhere, so maybe at an index where nums2 already has a very large number, because we are losing anyway.
Exactly! Now, let’s structure the approach systematically. First, sort nums1 to see what options are available:
nums1 (sorted) = [3, 5, 6, 7]
Next, also sort nums2, but remember the original indices by storing (value, index) pairs:
nums2 (sorted with indices) = [(2, 0), (4, 2), (8, 1), (10, 3)]
Now, the task is to pair elements from sorted nums1 with elements in sorted nums2 in the best way possible. Let’s try it step by step.
- Matching Smallest Possible Advantage: Take the smallest number in nums1 (3). Can it be placed somewhere beneficial?
- The smallest remaining number in nums2 is 2 (index 0), and 3 > 2, so assign 3 to index 0.
- Next Smallest Number: Now take 5 from nums1.
- The smallest remaining number in nums2 is 4 (index 2), and 5 > 4, so assign 5 to index 2.
- Next Smallest Number: Now take 6 from nums1.
- The smallest remaining number in nums2 is 8 (index 1), but 6 is not greater than 8.
- Since 6 cannot help, save it for a losing case and take the next number 7 instead.
- 7 is still not greater than 8, so keep it too. Now, only one option remains: assigning them to the largest remaining number (10, index 3).
- Assign 6 to index 3, and then assign 7 to index 1.
After placing all numbers, the final rearranged nums1 looks like:
ans = [3, 7, 5, 6]
So the strategy is to always try to give the smallest valid advantage, and if that’s not possible, sacrifice a number against the biggest remaining element.
This implementation sorts nums1, sorts nums2 while keeping track of original indices, and then processes assignments using a deque. This ensures efficient pairing while maintaining the greedy strategy.
Well summarized! Now, if you think about it, what kind of approach are we using here?
We are making the best possible choice at each step without looking ahead too much. This sounds like a greedy algorithm!
Exactly! The greedy approach works perfectly here because, at each step, we are ensuring that we maximize the number of indices where nums1[i] > nums2[i] without needing to explore all possible assignments exhaustively.
Let's now see how our algorithm looks!
Advantage Shuffle Algorithm
- Sort nums1 and nums2 → Allows efficient greedy allocation.
- Use a two-pointer greedy approach → Assign numbers optimally.
- Store remaining elements → Use them when no better assignment is available.
- Reconstruct the output → Place assigned numbers at correct positions.
Approach
- Sorting:
- First, we sort nums1 to allow optimal assignment.
- We also sort nums2 but keep track of the original indices to reconstruct the final result.
- Greedy Assignment:
- We iterate through sortedNums1 and try to assign each element optimally to sortedNums2.
- If nums1[i] > nums2[j], we assign nums1[i] to nums2[j] (maximize advantage).
- Otherwise, store the remaining elements for later use.
- Result Construction:
- We construct the output array using assigned values.
- If no optimal assignment exists for an index, we use the remaining elements.
- Update Conditions:
- If a number in nums1 can beat the smallest unassigned number in nums2, assign it.
- If no such number exists, assign the smallest remaining number.
- Maintain a deque to track unused elements.
Final Step: Return the final permutation of nums1 that maximizes its advantage over nums2.
Let us understand this with a video,
Dry-Run
Example Input:
nums1 = [9, 1, 5, 3]
nums2 = [4, 7, 2, 8]
Output: [5, 9, 3, 1]
Explanation
Step 1: Sorting
Sort nums1: sortedNums1 = [1, 3, 5, 9]
Sort nums2 but keep track of original indices:
sortedNums2 = [(2, 2), (4, 0), (7, 1), (8, 3)]
Here, (value, original_index) pairs indicate the original position in nums2.
Step 2: Greedy Assignment
We iterate through sortedNums1 and try to assign numbers optimally.
- 1 (smallest in nums1) cannot beat 2, so store it in remaining.
- 3 can beat 2, so assign 3 to nums2[2].
- 5 can beat 4, so assign 5 to nums2[0].
- 9 can beat 7, so assign 9 to nums2[1].
- Leftover number 1 goes to nums2[3].
Assignments: assigned = {2 → 3, 4 → 5, 7 → 9}
remaining = [1]
Step 3: Construct the Result Array
Using nums2 = [4, 7, 2, 8]'s original indices:
- nums2[0] = 4 → Assigned 5
- nums2[1] = 7 → Assigned 9
- nums2[2] = 2 → Assigned 3
- nums2[3] = 8 → No assigned number, take from remaining → 1
Final Output: [5, 9, 3, 1]
Advantage Shuffle Solution
Now let's checkout the "Advantage Shuffle code" in C++, Java, Python and JavaScript.
"Advantage Shuffle" Code in all Languages.
1. Advantage Shuffle solution in C++ Try on Compiler
class Solution {
public:
vector<int> advantageCount(vector<int>& nums1, vector<int>& nums2) {
// Sort nums1 to determine optimal assignments
vector<int> sortedNums1 = nums1;
sort(sortedNums1.begin(), sortedNums1.end());
// Sort nums2 while maintaining original indices
vector<pair<int, int>> sortedNums2;
for (int i = 0; i < nums2.size(); i++) {
sortedNums2.push_back({nums2[i], i});
}
sort(sortedNums2.begin(), sortedNums2.end());
// Map to store assigned elements for each nums2[i]
map<int, deque<int>> assigned;
for (int b : nums2) assigned[b] = {};
// Remaining elements that couldn't beat any nums2[i]
deque<int> remaining;
int j = 0;
// Assign elements from sortedNums1 to sortedNums2 optimally
for (int num : sortedNums1) {
if (num > sortedNums2[j].first) {
assigned[sortedNums2[j].first].push_back(num);
j++;
} else {
remaining.push_back(num);
}
}
vector<int> result(nums2.size());
// Construct the result array
for (int i = 0; i < nums2.size(); i++) {
if (!assigned[nums2[i]].empty()) {
result[i] = assigned[nums2[i]].front();
assigned[nums2[i]].pop_front();
} else {
result[i] = remaining.front();
remaining.pop_front();
}
}
return result;
}
};2. Advantage Shuffle Solution in Java Try on Compiler
class Solution {
public int[] advantageCount(int[] A, int[] B) {
// Sort A to determine optimal assignments
int[] sortedA = A.clone();
Arrays.sort(sortedA);
// Sort B while maintaining original indices
int[][] sortedB = new int[B.length][2];
for (int i = 0; i < B.length; i++) {
sortedB[i] = new int[]{B[i], i};
}
Arrays.sort(sortedB, Comparator.comparingInt(a -> a[0]));
// Map to store assigned elements for each B[i]
Map<Integer, Deque<Integer>> assigned = new HashMap<>();
for (int b : B) assigned.put(b, new LinkedList<>());
// Remaining elements that couldn't beat any B[i]
Deque<Integer> remaining = new LinkedList<>();
int j = 0;
// Assign elements from sortedA to sortedB optimally
for (int a : sortedA) {
if (a > sortedB[j][0]) {
assigned.get(sortedB[j][0]).add(a);
j++;
} else {
remaining.add(a);
}
}
int[] ans = new int[B.length];
// Construct the result array
for (int i = 0; i < B.length; i++) {
if (!assigned.get(B[i]).isEmpty()) {
ans[i] = assigned.get(B[i]).poll();
} else {
ans[i] = remaining.poll();
}
}
return ans;
}
}3. Advantage Shuffle Solution in Python Try on Compiler
class Solution:
def advantageCount(self, nums1: List[int], nums2: List[int]) -> List[int]:
# Sort nums1 to determine optimal assignments
sortedA = sorted(nums1)
# Sort nums2 while maintaining original indices
sortedB = sorted(enumerate(nums2), key=lambda x: x[1])
# Dictionary to store assigned elements for each nums2[i]
assigned = {b: deque() for b in nums2}
# Remaining elements that couldn't beat any nums2[i]
remaining = deque()
j = 0
# Assign elements from sortedA to sortedB optimally
for a in sortedA:
if a > sortedB[j][1]:
assigned[sortedB[j][1]].append(a)
j += 1
else:
remaining.append(a)
# Construct the result array
return [assigned[b].popleft() if assigned[b] else remaining.popleft() for b in nums2]
4. Advantage Shuffle solution in JavaScript Try on Compiler
/**
* @param {number[]} nums1
* @param {number[]} nums2
* @return {number[]}
*/
var advantageCount = function(nums1, nums2) {
// Sort nums1 to determine optimal assignments
let sortedA = [...nums1].sort((a, b) => a - b);
// Sort nums2 while maintaining original indices
let sortedB = nums2.map((num, index) => [num, index]).sort((a, b) => a[0] - b[0]);
// Map to store assigned elements for each nums2[i]
let assigned = new Map();
nums2.forEach(num => assigned.set(num, []));
// Remaining elements that couldn't beat any nums2[i]
let remaining = [];
let j = 0;
// Assign elements from sortedA to sortedB optimally
for (let a of sortedA) {
if (a > sortedB[j][0]) {
assigned.get(sortedB[j][0]).push(a);
j++;
} else {
remaining.push(a);
}
}
// Construct the result array
return nums2.map(b => assigned.get(b).length ? assigned.get(b).shift() : remaining.shift());
};Advantage Shuffle Complexity Analysis
Time Complexity: O(n log n)
The Advantage Shuffle algorithm involves three main operations:
- Sorting nums1 and nums2
→ Sorting takes O(n log n) time for both arrays, where n is the length of nums1 (same as nums2). - Greedy Assignment of Elements
→ We iterate through the sorted nums1 and try to assign elements to nums2, which takes O(n) time. - Reconstructing the Output Array
→ Another pass through nums2 to construct the final answer, which also takes O(n) time.
Thus, the total time complexity is: O(n log n)+O(n)+O(n) = O(n log n)
Space Complexity: O(n)
Auxiliary Space Complexity
- We use maps and deques to track assignments and remaining elements.
- However, all these structures store at most n elements, leading to O(n) auxiliary space.
Total Space Complexity
- Input storage: O(n) (since nums1 and nums2 are given).
- Sorting is done in separate arrays, requiring O(n) extra space.
- Result array: O(n).
Thus, the total space complexity is O(n)
Similar Problems
Given an array of intervals intervals where intervals[i] = [starti, endi], return the minimum number of intervals you need to remove to make the rest of the intervals non-overlapping.
Note that intervals which only touch at a point are non-overlapping. For example, [1, 2] and [2, 3] are non-overlapping.
A company is planning to interview 2n people. Given the array costs where costs[i] = [aCosti, bCosti], the cost of flying the ith person to city a is aCosti, and the cost of flying the ith person to city b is bCosti.
Return the minimum cost to fly every person to a city such that exactly n people arrive in each city.