4Sum Solution In C++/Java/Python/JS
Problem Description
Given an array nums of nn integers, return an array of all the unique quadruplets [nums[a], nums[b], nums[c], nums[d]] such that:
0 ≤ a,b,c,d < n
a,b,c and d are distinct indices
nums[a] + nums[b] + nums[c] + nums[d] = target
You may return the answer in any order.
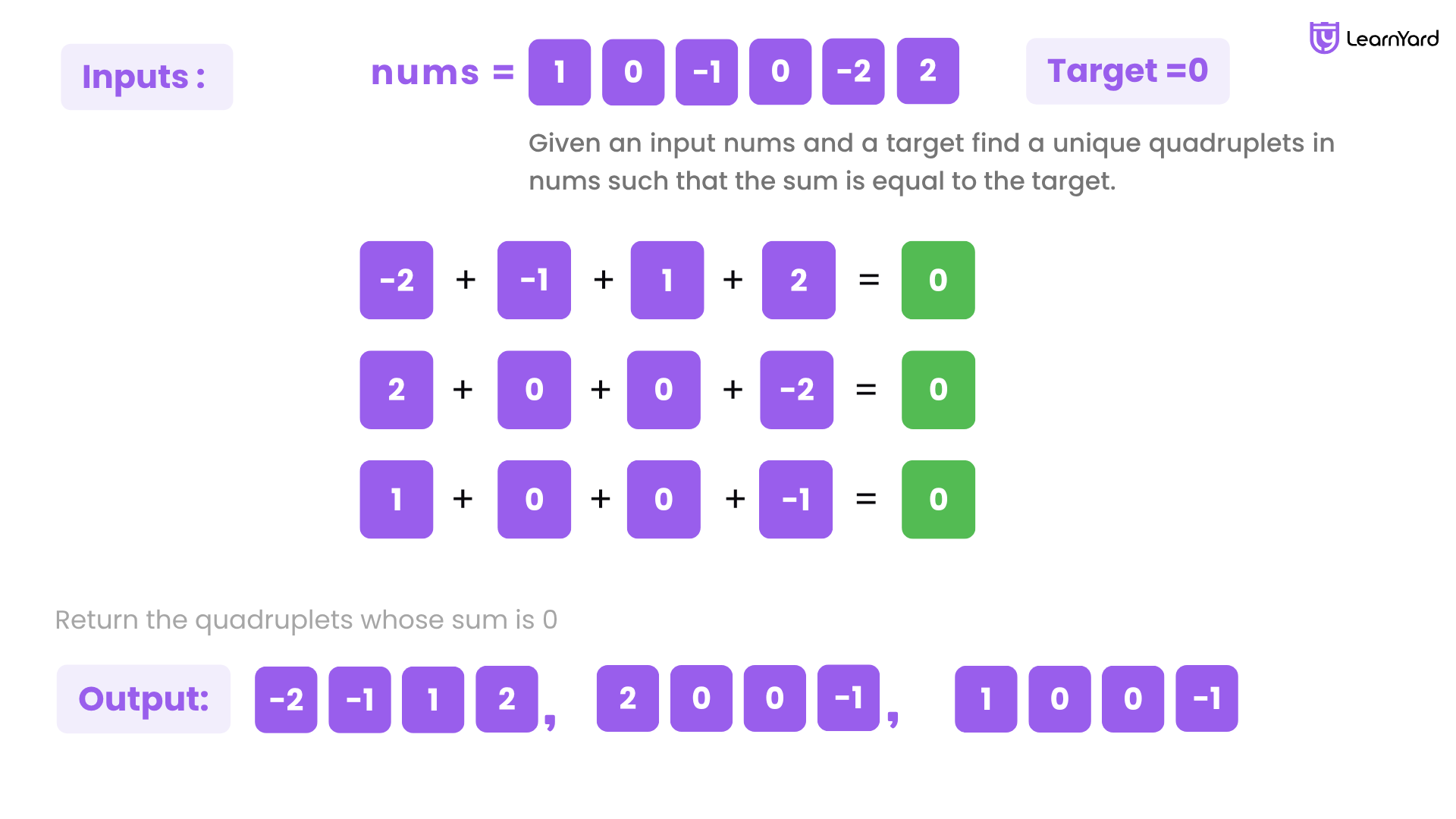
Examples:
Input : nums = [1, 0, -1, 0, -2, 2], target = 0
Output:[[-2, -1, 1, 2], [-2, 0, 0, 2], [-1, 0, 0, 1]]
Input : nums = [2, 2, 2, 2, 2], target = 8
Output:[[2, 2, 2, 2]]
Constraints:
- 1 <= nums.length <= 200
- -10^9 <= nums[i] <= 10^9
- -10^9 <= target <= 10^9
This problem is straightforward yet challenging, requiring all unique quadruplets that sum to a target value. The task is to explore combinations efficiently while handling duplicates, leveraging sorting and pointers to optimize the solution for large inputs.
Brute Force Approach
Intuition
The brute force approach to solving the 4Sum problem involves systematically checking every combination of four numbers in the array. The goal is to identify all unique quadruplets that sum up to the target value.
To achieve this, we use four nested loops. The first loop selects the first number, the second chooses the second number, the third selects the third, and the fourth picks the fourth. For each combination, we calculate the sum of the four numbers and check if it matches the target. If it does, the quadruplet is stored in a result list.
To ensure the result contains only unique quadruplets, we utilize a set to store them. Since sets inherently avoid duplicates, adding quadruplets as tuples to the set guarantees that each combination is unique, even if the array contains repeated elements. After processing all combinations, the set is converted back to a list of lists to provide the final result.
This approach is ensuring every possible group of four numbers is evaluated . It provides a clear understanding of the problem by focusing on breaking it into smaller, manageable steps: selecting numbers, calculating their sum, and filtering unique combinations .
What is Set?
A set is a collection in programming that automatically enforces uniqueness. Unlike arrays or lists, where duplicates can exist, a set ensures that each element appears only once. This is particularly useful in scenarios where you need to eliminate repeated values, such as ensuring all triplets are unique in this problem.
Approach
Step 1: Initialize an empty set
Create an empty set to store quadruplets. Using a set ensures no duplicates are added as it inherently handles uniqueness.
Step 2: Pick the first number using the outer loop
Iterate over the array for the first number (i). The loop starts from the first element and goes up to the fourth-last element to ensure room for other numbers.
Step 3: Pick the second number using the second loop
For each first number, use a second loop to pick the second number (j). Start from i + 1 and go up to the third-last element.
Step 4: Pick the third number using the third loop
For each pair of nums[i] and nums[j], use a third loop to pick the third number (k). Start from j + 1 and go up to the second-last element.
Step 5: Pick the fourth number using the fourth loop
For each triplet of nums[i], nums[j], and nums[k], use a fourth loop to pick the fourth number (l). Start from k + 1 and iterate through the remaining elements.
Step 6: Check the sum of the quadruplet
Calculate the sum of the four selected numbers. If it matches the target value, add the quadruplet (as a tuple) to the set.
Step 7: Convert set to list
Convert the set of quadruplets into a list of lists, as the final result should be in list format instead of tuples.
4Sum-Brute-Force-Approach
4Sum Dry run - BruteForce
Input : nums = [1, 0, -1, 0, -2, 2] target = 0
Step 1: Initialize the result set
We start with an empty set to store the unique quadruplets. result = set()
Step 2: Iterate through all possible combinations of four numbers
We use four nested loops to check every combination of four numbers from the array. For each combination, we calculate the sum and check if it equals the target. If the sum is equal to the target, we add the quadruplet to the result set.
First combination: (1, 0, -1, 0)
- i = 0, j = 1, k = 2, l = 3
- Sum: 1 + 0 + (-1) + 0 = 0
- The sum matches the target (0), so add (1, 0, -1, 0) to the result set.result = {(1, 0, -1, 0)}
Second combination: (1, 0, -1, -2)
- i = 0, j = 1, k = 2, l = 4
- Sum: 1 + 0 + (-1) + (-2) = -2
- The sum does not match the target, continue to the next combination.
Third combination: (1, 0, -1, 2)
- i = 0, j = 1, k = 2, l = 5
- Sum: 1 + 0 + (-1) + 2 = 2
- The sum does not match the target, continue to the next combination.
Fourth combination: (1, 0, 0, -2)
- i = 0, j = 1, k = 3, l = 4
- Sum: 1 + 0 + 0 + (-2) = -1
- The sum does not match the target, continue to the next combination.
Fifth combination: (1, 0, 0, 2)
- i = 0, j = 1, k = 3, l = 5
- Sum: 1 + 0 + 0 + 2 = 3
- The sum does not match the target, continue to the next combination.
Sixth combination: (1, -1, 0, -2)
- i = 0, j = 2, k = 3, l = 4
- Sum: 1 + (-1) + 0 + (-2) = -2
- The sum does not match the target, continue to the next combination.
Seventh combination: (1, -1, 0, 2)
- i = 0, j = 2, k = 3, l = 5
- Sum: 1 + (-1) + 0 + 2 = 2
- The sum does not match the target, continue to the next combination.
Eighth combination: (1, -1, 0, -2)
- i = 0, j = 2, k = 4, l = 5
- Sum: 1 + (-1) + 0 + (-2) = -2
- The sum does not match the target, continue to the next combination.
Ninth combination: (0, -1, 0, -2)
- i = 1, j = 2, k = 3, l = 4
- Sum: 0 + (-1) + 0 + (-2) = -3
- The sum does not match the target, continue to the next combination.
Tenth combination: (0, -1, 0, 2)
- i = 1, j = 2, k = 3, l = 5
- Sum: 0 + (-1) + 0 + 2 = 1
- The sum does not match the target, continue to the next combination.
Eleventh combination: (0, 0, -2, 2)
- i = 1, j = 3, k = 4, l = 5
- Sum: 0 + 0 + (-2) + 2 = 0
- The sum matches the target (0), so add (0, 0, -2, 2) to the result set.result = {(0, 0, -2, 2), (1, 0, -1, 0)}
Twelfth combination: (-1, 0, 0, 1)
- i = 2, j = 3, k = 4, l = 5
- Sum: -1 + 0 + 0 + 1 = 0
- The sum matches the target (0), so add (-1, 0, 0, 1) to the result set.result = {(-2, -1, 1, 2), (-2, 0, 0, 2), (-1, 0, 0, 1), (1, 0, -1, 0), (0, 0, -2, 2)}
Final Result:
After checking all combinations, we find the unique quadruplets that sum to 0. These quadruplets are:
{(-2, -1, 1, 2), (-2, 0, 0, 2), (-1, 0, 0, 1)}
Therefore, the final result is: [(-2, -1, 1, 2), (-2, 0, 0, 2), (-1, 0, 0, 1)]
4Sum Code for All Languages - BruteForce
C++
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
// Step 1: Initialize an empty set
unordered_set<string> uniqueQuadruplets;
vector<vector<int>> result;
int n = nums.size();
// Sort the array to ensure unique quadruplets
sort(nums.begin(), nums.end());
// Step 2: Pick the first number using the outer loop
for (int i = 0; i < n - 3; i++) {
// Step 3: Pick the second number using the second loop
for (int j = i + 1; j < n - 2; j++) {
// Step 4: Pick the third number using the third loop
for (int k = j + 1; k < n - 1; k++) {
// Step 5: Pick the fourth number using the fourth loop
for (int l = k + 1; l < n; l++) {
// Step 6: Check the sum of the quadruplet
int sum = nums[i] + nums[j] + nums[k] + nums[l];
if (sum == target) {
// Step 7: Convert set to list (add to result only if not already in the set)
string quadruplet = to_string(nums[i]) + "," + to_string(nums[j]) + "," + to_string(nums[k]) + "," + to_string(nums[l]);
if (uniqueQuadruplets.find(quadruplet) == uniqueQuadruplets.end()) {
result.push_back({nums[i], nums[j], nums[k], nums[l]});
uniqueQuadruplets.insert(quadruplet);
}
}
}
}
}
}
return result;
}
};4Sum code in Java - BruteForce
public class FourSum {
public static class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
// Step 1: Initialize an empty set
Set<String> uniqueQuadruplets = new HashSet<>();
List<List<Integer>> result = new ArrayList<>();
int n = nums.length;
// Sort the array to ensure unique quadruplets
Arrays.sort(nums);
// Step 2: Pick the first number using the outer loop
for (int i = 0; i < n - 3; i++) {
// Step 3: Pick the second number using the second loop
for (int j = i + 1; j < n - 2; j++) {
// Step 4: Pick the third number using the third loop
for (int k = j + 1; k < n - 1; k++) {
// Step 5: Pick the fourth number using the fourth loop
for (int l = k + 1; l < n; l++) {
// Step 6: Check the sum of the quadruplet
int sum = nums[i] + nums[j] + nums[k] + nums[l];
if (sum == target) {
// Step 7: Convert set to list (add to result only if not already in the set)
String quadruplet = nums[i] + "," + nums[j] + "," + nums[k] + "," + nums[l];
if (!uniqueQuadruplets.contains(quadruplet)) {
result.add(Arrays.asList(nums[i], nums[j], nums[k], nums[l]));
uniqueQuadruplets.add(quadruplet);
}
}
}
}
}
}
return result;
}
}4Sum code in Python - BruteForce
def four_sum(nums, target):
# Step 1: Initialize an empty set
unique_quadruplets = set()
result = []
# Sort the array to ensure unique quadruplets
nums.sort()
# Step 2: Pick the first number using the outer loop
for i in range(len(nums) - 3):
# Step 3: Pick the second number using the second loop
for j in range(i + 1, len(nums) - 2):
# Step 4: Pick the third number using the third loop
for k in range(j + 1, len(nums) - 1):
# Step 5: Pick the fourth number using the fourth loop
for l in range(k + 1, len(nums)):
# Step 6: Check the sum of the quadruplet
current_sum = nums[i] + nums[j] + nums[k] + nums[l]
if current_sum == target:
# Step 7: Convert set to list (add to result only if not already in the set)
quadruplet = (nums[i], nums[j], nums[k], nums[l])
if quadruplet not in unique_quadruplets:
result.append([nums[i], nums[j], nums[k], nums[l]])
unique_quadruplets.add(quadruplet)
return result
4Sum code in Javascript - BruteForce
function fourSum(nums, target) {
// Step 1: Initialize an empty set
let uniqueQuadruplets = new Set();
let result = [];
// Sort the array to ensure unique quadruplets
nums.sort((a, b) => a - b);
// Step 2: Pick the first number using the outer loop
for (let i = 0; i < nums.length - 3; i++) {
// Step 3: Pick the second number using the second loop
for (let j = i + 1; j < nums.length - 2; j++) {
// Step 4: Pick the third number using the third loop
for (let k = j + 1; k < nums.length - 1; k++) {
// Step 5: Pick the fourth number using the fourth loop
for (let l = k + 1; l < nums.length; l++) {
// Step 6: Check the sum of the quadruplet
let currentSum = nums[i] + nums[j] + nums[k] + nums[l];
if (currentSum === target) {
// Step 7: Convert set to list (add to result only if not already in the set)
let quadruplet = [nums[i], nums[j], nums[k], nums[l]].sort((a, b) => a - b).toString();
if (!uniqueQuadruplets.has(quadruplet)) {
result.push([nums[i], nums[j], nums[k], nums[l]]);
uniqueQuadruplets.add(quadruplet);
}
}
}
}
}
}
return result;
}
Time Complexity: O(n^4)
The brute force approach involves checking all possible quadruplets in the array. Since the array has n elements, we need to check every combination of four numbers. This can be broken down as:
- The first loop runs n times, selecting the first number.
- The second loop runs n-1 times, selecting the second number.
- The third loop runs n-2 times, selecting the third number.
- The fourth loop runs n-3 times, selecting the fourth number.
Thus, the total number of combinations is O(n^4), because we are iterating through all quadruplets, resulting in a time complexity of O(n^4).
Space Complexity:O(N^4)
Auxiliary Space Complexity:
The algorithm uses a few variables for iteration, which takes constant space, O(1). The set for storing quadruplets is part of the output, not auxiliary space.
Thus, auxiliary space is O(1).
Total Space Complexity:
The input array nums takes O(n) space. The set to store unique quadruplets can store up to O(n4) quadruplets.
Thus, total space complexity is O(n^4).
Optimal Approach : Hashset
Intuition
To solve this problem more efficiently, we need to avoid checking all possible combinations, which takes too much time. Instead of using four loops, we can fix three numbers and calculate the fourth one. This helps reduce extra work and makes the solution faster.
We can find the fourth number by using the formula: lastNumber = target - (nums[i] + nums[j] + nums[k]). If we have already seen this number before, it means we found a valid combination. To check this quickly, we can use a HashSet to store past numbers.
Using a HashSet helps us check if the required number exists in constant time. As we go through the numbers, we add them to the set. This way, when processing three numbers, we can quickly check if the fourth number is available.
This approach makes the solution much faster, reducing the time needed to find all quadruplets. Instead of checking every combination, we focus only on useful ones. By using the HashSet, we avoid repeating work and improve performance.
what is a Hashset ?
A HashSet is a data structure that stores unique elements in an unordered way. It provides fast operations like adding, removing, and checking elements using a hashing mechanism. HashSet is useful when quick lookups and uniqueness of elements are required, with average O(1) time complexity.
Approach
Step 1: Sort the array
Sort the array to simplify finding combinations and avoid duplicates. Sorting ensures a structured order, making it easier to process elements efficiently.
Step 2: Fix the first two numbers
Use two nested loops to fix the first two numbers, reducing the problem to finding two remaining numbers that sum up to the target.
Step 3: Use a HashSet to track elements
Create a HashSet to store seen numbers, allowing quick lookups to check if the required fourth number exists without searching the entire array.
Step 4: Calculate the required fourth number
Compute the fourth number using the formula:
lastNumber=target−(nums[i]+nums[j]+nums[k])
This helps identify the needed value.
Step 5: Check if the fourth number exists
If the calculated fourth number is in the HashSet, store the quadruplet in a result set to ensure uniqueness and avoid duplicate combinations.
Step 6: Add the current number to the HashSet
Add the current number to the HashSet for future checks, ensuring efficient lookups for upcoming iterations without reprocessing elements.
Step 7: Convert the result set to a list
Convert the result set to a sorted list of lists to meet the output format requirements and return the unique quadruplets.
4Sum Dry run - Optimised (Hashmap)
Input:nums = [1, 0, -1, 0, -2, 2]target = 0
Step 1: Sort the array
Sorted nums = [-2, -1, 0, 0, 1, 2]
Step 2: Fix the first two numbers
We iterate over nums[i] and nums[j] using two loops.
Iteration 1: i = 0 (nums[i] = -2), j = 1 (nums[j] = -1)
- Initialize an empty HashSet: seen = {}
- Target sum to be achieved: 0 - (-2 + -1) = 3
Sub-iteration over k:
- k = 2 (nums[k] = 0), required lastNumber = 3 - 0 = 3 (not in seen) → Add 0 to seen → seen = {0}
- k = 3 (nums[k] = 0), required lastNumber = 3 - 0 = 3 (not in seen) → Add 0 to seen → seen = {0}
- k = 4 (nums[k] = 1), required lastNumber = 3 - 1 = 2 (not in seen) → Add 1 to seen → seen = {0, 1}
- k = 5 (nums[k] = 2), required lastNumber = 3 - 2 = 1 (1 found in seen) → Add quadruplet (-2, -1, 1, 2)
Result so far: result = {(-2, -1, 1, 2)}
Iteration 2: i = 0 (nums[i] = -2), j = 2 (nums[j] = 0)
- Initialize an empty HashSet: seen = {}
- Target sum to be achieved: 0 - (-2 + 0) = 2
Sub-iteration over k:
- k = 3 (nums[k] = 0), required lastNumber = 2 - 0 = 2 (not in seen) → Add 0 to seen → seen = {0}
- k = 4 (nums[k] = 1), required lastNumber = 2 - 1 = 1 (not in seen) → Add 1 to seen → seen = {0, 1}
- k = 5 (nums[k] = 2), required lastNumber = 2 - 2 = 0 (0 found in seen) → Add quadruplet (-2, 0, 0, 2)
Result so far: result = {(-2, -1, 1, 2), (-2, 0, 0, 2)}
Iteration 3: i = 1 (nums[i] = -1), j = 2 (nums[j] = 0)
- Initialize an empty HashSet: seen = {}
- Target sum to be achieved: 0 - (-1 + 0) = 1
Sub-iteration over k:
- k = 3 (nums[k] = 0), required lastNumber = 1 - 0 = 1 (not in seen) → Add 0 to seen → seen = {0}
- k = 4 (nums[k] = 1), required lastNumber = 1 - 1 = 0 (0 found in seen) → Add quadruplet (-1, 0, 0, 1)
Result so far: result = {(-2, -1, 1, 2), (-2, 0, 0, 2), (-1, 0, 0, 1)}
Step 7: Convert result set to a list
Finally, the result set {(-2, -1, 1, 2), (-2, 0, 0, 2), (-1, 0, 0, 1)} is converted into a sorted list of lists:
Output:[[-2, -1, 1, 2], [-2, 0, 0, 2], [-1, 0, 0, 1]]
Thus, the quadruplets that sum up to 0 are:[[-2, -1, 1, 2], [-2, 0, 0, 2], [-1, 0, 0, 1]]
4Sum Code for All Languages - Optimised (Hashmap)
C++
vector<vector<int>> fourSum(vector<int>& nums, int target) {
// Step 1: Sort the array
sort(nums.begin(), nums.end());
vector<vector<int>> result;
// Step 2: Fix the first two numbers
for (int i = 0; i < nums.size() - 3; i++) {
// Skip duplicate values for the first number
if (i > 0 && nums[i] == nums[i - 1]) continue;
for (int j = i + 1; j < nums.size() - 2; j++) {
// Skip duplicate values for the second number
if (j > i + 1 && nums[j] == nums[j - 1]) continue;
// Step 3: Use a HashSet to track elements
unordered_set<int> seen;
// Step 4: Calculate the required fourth number
for (int k = j + 1; k < nums.size(); k++) {
int lastNumber = target - (nums[i] + nums[j] + nums[k]);
// Step 5: Check if the fourth number exists
if (seen.find(lastNumber) != seen.end()) {
result.push_back({nums[i], nums[j], nums[k], lastNumber});
// Step 6: Skip duplicate values for the third number
while (k + 1 < nums.size() && nums[k] == nums[k + 1]) {
k++;
}
}
// Add the current number to the HashSet
seen.insert(nums[k]);
}
}
}
// Step 7: Return the result list
return result;
}4Sum Code in Java - Optimised (Hashmap)
public class FourSum {
public static List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> result = new ArrayList<>();
int n = nums.length;
// Step 1: Sort the array
Arrays.sort(nums);
// Step 2: Fix the first two numbers
for (int i = 0; i < n - 3; i++) {
if (i > 0 && nums[i] == nums[i - 1]) continue; // Skip duplicates
for (int j = i + 1; j < n - 2; j++) {
if (j > i + 1 && nums[j] == nums[j - 1]) continue; // Skip duplicates
int left = j + 1, right = n - 1;
while (left < right) {
int sum = nums[i] + nums[j] + nums[left] + nums[right];
if (sum == target) {
result.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
// Move left and right pointers to avoid duplicates
while (left < right && nums[left] == nums[left + 1]) left++;
while (left < right && nums[right] == nums[right - 1]) right--;
left++;
right--;
} else if (sum < target) {
left++;
} else {
right--;
}
}
}
}
return result;
}
4Sum Code in Python - Optimised (Hashmap)
class Solution:
def fourSum(self, nums, target):
# Step 1: Sort the array
nums.sort()
result = []
# Step 2: Fix the first two numbers
for i in range(len(nums) - 3):
for j in range(i + 1, len(nums) - 2):
# Step 3: Use a HashSet to track elements
seen = set()
# Step 4: Calculate the required fourth number
for k in range(j + 1, len(nums) - 1):
lastNumber = target - (nums[i] + nums[j] + nums[k])
# Step 5: Check if the fourth number exists
if lastNumber in seen:
result.append([nums[i], nums[j], nums[k], lastNumber])
# Step 6: Add the current number to the HashSet
seen.add(nums[k])
# Skip duplicates for the second number
while j + 1 < len(nums) and nums[j] == nums[j + 1]:
j += 1
# Skip duplicates for the first number
while i + 1 < len(nums) and nums[i] == nums[i + 1]:
i += 1
# Step 7: Convert the result set to a list
return result
4Sum Code in Javascript - Optimised (Hashmap)
class Solution {
fourSum(nums, target) {
// Step 1: Sort the array
nums.sort((a, b) => a - b);
let result = [];
// Step 2: Fix the first two numbers
for (let i = 0; i < nums.length - 3; i++) {
for (let j = i + 1; j < nums.length - 2; j++) {
// Step 3: Use a HashSet to track elements
let seen = new Set();
// Step 4: Calculate the required fourth number
for (let k = j + 1; k < nums.length - 1; k++) {
let lastNumber = target - (nums[i] + nums[j] + nums[k]);
// Step 5: Check if the fourth number exists
if (seen.has(lastNumber)) {
result.push([nums[i], nums[j], nums[k], lastNumber]);
}
// Step 6: Add the current number to the HashSet
seen.add(nums[k]);
}
// Skip duplicates for the second number
while (j + 1 < nums.length && nums[j] === nums[j + 1]) {
j++;
}
}
// Skip duplicates for the first number
while (i + 1 < nums.length && nums[i] === nums[i + 1]) {
i++;
}
}
// Step 7: Convert the result set to a list
return result;
}
}Time Complexity: O(N^3)
Outer Loop: The solution involves three nested loops for selecting three numbers. The outer loop (i loop) runs for all N elements in the array, so it will run O(N) times.
Second Loop (j loop): For each i, the second loop (j loop) also runs O(N) times, and similarly, the third loop (k loop) runs O(N) times.Hence, the total number of iterations for the three loops combined is O(N^3).
HashSet Operations: For each combination of (i, j, k), we compute the required fourth number, lastNumber = target - (nums[i] + nums[j] + nums[k]), and check if it exists in the HashSet. This check and insertion in the HashSet take constant time, i.e., O(1).So, the time complexity for HashSet operations does not increase the overall time complexity of the solution.
Therefore, the overall time complexity is dominated by the three nested loops and is : O(N^3)
Space Complexity: O(n^2)
Auxiliary Space Complexity : O(n^2)
HashSet : Each inner loop uses a Set to track elements, which in the worst case can store O(n) elements.
Result Storage (result): In the worst case, all unique quadruplets are stored, leading to O(n^2) space in the result array.
Total Space Complexity : O(n^2)
The input array requires O(n) space.
The result list can store O(n^2) quadruplets in the worst case.
Optimal Approach : Two Pointer
Intuition
A brute-force approach would involve checking all possible combinations of four numbers, resulting in an inefficient O(n⁴) time complexity. Instead, we can optimize our approach by fixing two numbers and then solving a reduced 2Sum problem using the two-pointer technique. This significantly reduces the number of checks needed and improves efficiency.
By first sorting the array, we can easily handle duplicates and enable the two-pointer approach. The sorting step ensures that numbers are in a fixed order, allowing us to efficiently traverse and compare sums. We begin by iterating through the array and selecting the first and second numbers (nums[i] and nums[j]). After fixing these two numbers, our task reduces to finding two more numbers (nums[low] and nums[high]) such that their sum equals target - (nums[i] + nums[j]).
The two-pointer technique is key to solving this efficiently. We initialize low just after j and high at the end of the array. If the sum of the four numbers is less than the target, we increment low to increase the sum. If the sum is greater thanthe target, we decrement high to reduce the sum. If a valid quadruplet is found, we add it to the result and move both pointers past duplicate values to avoid counting the same combination multiple times.
By combining these ideas—sorting the array, fixing two numbers, and solving the remaining problem using two pointers—we achieve an efficient O(n³) time complexity, which is a significant improvement over the brute-force O(n⁴) approach. This method ensures that we only check necessary combinations while maintaining correctness and avoiding duplicate quadruplets.
Approach
Step 1: Sort the Array
Sorting the array makes it easier to find unique quadruplets and helps efficiently use the two-pointer approach. Sorting ensures elements are in non-decreasing order, allowing us to traverse and compare sums systematically.
Step 2: Iterate Over the First Element
Use a loop to fix the first number, nums[i]. Since we need four numbers in total, we stop the loop at n-3. To avoid duplicate quadruplets, we skip duplicate values by checking if nums[i] == nums[i-1].
Step 3: Iterate Over the Second Element
After fixing nums[i], iterate over the second number, nums[j]. This loop runs from i+1 to n-2 since we still need two more numbers. Again, we skip duplicate values by checking if nums[j] == nums[j-1].
Step 4: Use Two Pointers to Find the Remaining Two Numbers
Once we have fixed nums[i] and nums[j], we use two pointers:
- low, starting from j+1.
- high, starting from the last index n-1.
The goal is to find two numbers such that nums[i] + nums[j] + nums[low] + nums[high] == target.
Step 5: Adjust Pointers Based on the Sum
- If the sum of the four numbers is less than the target, increment low to increase the sum.
- If the sum is greater than the target, decrement high to decrease the sum.
- If the sum matches the target, store the quadruplet and move both low and high pointers past duplicate values to avoid redundant results.
Step 6: Skip Duplicate Quadruplets
After finding a valid quadruplet, we move low forward while nums[low] == nums[low+1] to skip duplicates. Similarly, we move high backward while nums[high] == nums[high-1].
Step 7: Continue Searching Until All Unique Quadruplets Are Found
Once we process all possible quadruplets, return the list containing unique sets of four numbers that sum to the target.
4Sum Dry run - Optimised (Two Pointer)
Input: nums = [1, 0, -1, 0, -2, 2]target = 0
Step 1: Sorting the Array
Sorting helps in avoiding duplicates and efficiently using the two-pointer approach.
Sorted nums: [-2, -1, 0, 0, 1, 2]
Step 2: Iterating through the array
We fix two numbers and use two pointers to find the remaining two.
First iteration (i = 0, fixed num = -2)
- Second number (j = 1, fixed num = -1)
- low = 2, high = 5
- current_sum = -2 + (-1) + 0 + 2 = -1 (less than target, move low right)
- low = 3 , high = 5
- current_sum = -2 + (-1) + 0 + 2 = -1 (still less, move low right)
- low = 4, high = 5
- current_sum = -2 + (-1) + 1 + 2 = 0 (matches target, store [-2, -1, 1, 2])
- Move low right to avoid duplicates
Second number (j = 2, fixed num = 0)
- low = 3, high = 5
- current_sum = -2 + 0 + 0 + 2 = 0 (matches target, store [-2, 0, 0, 2])
- Move low right to avoid duplicates
Second number (j = 3, fixed num = 0, duplicate detected, skip it)
Second iteration (i = 1, fixed num = -1)
Second number (j = 2, fixed num = 0)
- low = 3, high = 5
- current_sum = -1 + 0 + 0 + 2 = 1 (greater than target, move high left)
- low = 3, high = 4
- current_sum = -1 + 0 + 0 + 1 = 0 (matches target, store [-1, 0, 0, 1])
- Move low right to avoid duplicates
Second number (j = 3, fixed num = 0, duplicate detected, skip it)
Remaining iterations (i = 2 and onwards) don't find new unique quadrupletsFinal Output: [[-2, -1, 1, 2], [-2, 0, 0, 2], [-1, 0, 0, 1]]
4Sum Code for All Languages - Optimised (Two Pointer)
C++
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
int n = nums.size();
// Sort the array to enable the two-pointer approach
sort(nums.begin(), nums.end());
vector<vector<int>> result;
// Iterate over the first element
for (int i = 0; i < n - 3; i++) {
// Skip duplicate elements to avoid duplicate quadruplets
if (i > 0 && nums[i] == nums[i - 1]) continue;
// Iterate over the second element
for (int j = i + 1; j < n - 2; j++) {
// Skip duplicate elements to avoid duplicate quadruplets
if (j > i + 1 && nums[j] == nums[j - 1]) continue;
int low = j + 1, high = n - 1;
// Use two-pointer approach to find the remaining two elements
while (low < high) {
long long sum = (long long)nums[i] + nums[j] + nums[low] + nums[high];
// If the sum is less than target, move the left pointer
if (sum < target) {
low++;
}
// If the sum is greater than target, move the right pointer
else if (sum > target) {
high--;
}
// If a valid quadruplet is found, add it to the result
else {
result.push_back({nums[i], nums[j], nums[low], nums[high]});
// Move pointers to skip duplicate elements
while (low < high && nums[low] == nums[low + 1]) low++;
while (low < high && nums[high] == nums[high - 1]) high--;
low++;
high--;
}
}
}
}
return result;
}
};4Sum code in Java - Optimised (Two Pointer)
import java.util.*;
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
// Sort the array to simplify finding quadruplets
Arrays.sort(nums);
List<List<Integer>> result = new ArrayList<>();
int n = nums.length;
// Iterate over the first element
for (int i = 0; i < n - 3; i++) {
// Skip duplicate elements
if (i > 0 && nums[i] == nums[i - 1]) continue;
// Iterate over the second element
for (int j = i + 1; j < n - 2; j++) {
// Skip duplicate elements
if (j > i + 1 && nums[j] == nums[j - 1]) continue;
int low = j + 1, high = n - 1;
// Use two-pointer approach
while (low < high) {
long sum = (long) nums[i] + nums[j] + nums[low] + nums[high];
if (sum < target) {
low++;
} else if (sum > target) {
high--;
} else {
result.add(Arrays.asList(nums[i], nums[j], nums[low], nums[high]));
// Skip duplicate elements
while (low < high && nums[low] == nums[low + 1]) low++;
while (low < high && nums[high] == nums[high - 1]) high--;
low++;
high--;
}
}
}
}
return result;
}
}4Sum code in Python - Optimised (Two Pointer)
from typing import List
class Solution:
def fourSum(self, nums: List[int], target: int) -> List[List[int]]:
# Sort the array to use the two-pointer approach
nums.sort()
result = []
n = len(nums)
# Iterate over the first element
for i in range(n - 3):
if i > 0 and nums[i] == nums[i - 1]:
continue
# Iterate over the second element
for j in range(i + 1, n - 2):
if j > i + 1 and nums[j] == nums[j - 1]:
continue
low, high = j + 1, n - 1
# Use two-pointer approach
while low < high:
total = nums[i] + nums[j] + nums[low] + nums[high]
if total < target:
low += 1
elif total > target:
high -= 1
else:
result.append([nums[i], nums[j], nums[low], nums[high]])
while low < high and nums[low] == nums[low + 1]:
low += 1
while low < high and nums[high] == nums[high - 1]:
high -= 1
low += 1
high -= 1
return result
4Sum code in JavaScript - Optimised (Two Pointer)
var fourSum = function(nums, target) {
// Sort the array to apply two-pointer technique
nums.sort((a, b) => a - b);
let result = [];
let n = nums.length;
// Iterate over the first element
for (let i = 0; i < n - 3; i++) {
if (i > 0 && nums[i] === nums[i - 1]) continue;
// Iterate over the second element
for (let j = i + 1; j < n - 2; j++) {
if (j > i + 1 && nums[j] === nums[j - 1]) continue;
let low = j + 1, high = n - 1;
// Use two-pointer approach
while (low < high) {
let sum = nums[i] + nums[j] + nums[low] + nums[high];
if (sum < target) {
low++;
} else if (sum > target) {
high--;
} else {
result.push([nums[i], nums[j], nums[low], nums[high]]);
while (low < high && nums[low] === nums[low + 1]) low++;
while (low < high && nums[high] === nums[high - 1]) high--;
low++;
high--;
}
}
}
}
return result;
};Time Complexity: O(N3)
Sorting the array: O(NlogN)
Iterating over the first element (i): O(N)
Iterating over the second element (j): O(N)
Two-pointer search for remaining two elements (low,high): O(N)
Thus, the overall complexity: O(NlogN)+O(N3 )=O(N3)
Space Complexity: O(n2)
Auxiliary Space Complexity:
- Sorting is done in-place, so no extra space is used for that.
- The two-pointer approach only requires a few extra variables (O(1)).
- The output list stores unique quadruplets, which in the worst case can be O(N2) (if all quadruplets are unique).
Total Space Complexity:O(N2)
- Total space:
- O(N
- 2
- ) (in the worst case).
- Includes the input array (O(N)) and the auxiliary space (O(N2)).
Learning Tip
Now we have successfully tackled this problem, let's try these similar problems.
Given a 0-indexed integer array nums, return the number of distinct quadruplets (a, b, c, d) such that:nums[a] + nums[b] + nums[c] == nums[d], and a < b < c < d
Given four integer arrays nums1, nums2, nums3, and nums4 all of length n, return the number of tuples (i, j, k, l) such that:
0 <= i, j, k, l < nnums1[i] + nums2[j] + nums3[k] + nums4[l] == 0