2D-Arrays IV
We’ve covered how to add and subtract two matrices, print the upper and lower triangles of a matrix, and print both the left and right diagonals. These fundamental matrix operations serve as the building blocks for more complex algorithms. But did we miss to traverse the 2d-array in the boundaries ?? Let's learn how we gonna do that !!
Q12. Print the Boundary of a 2D-Array
Example
Input
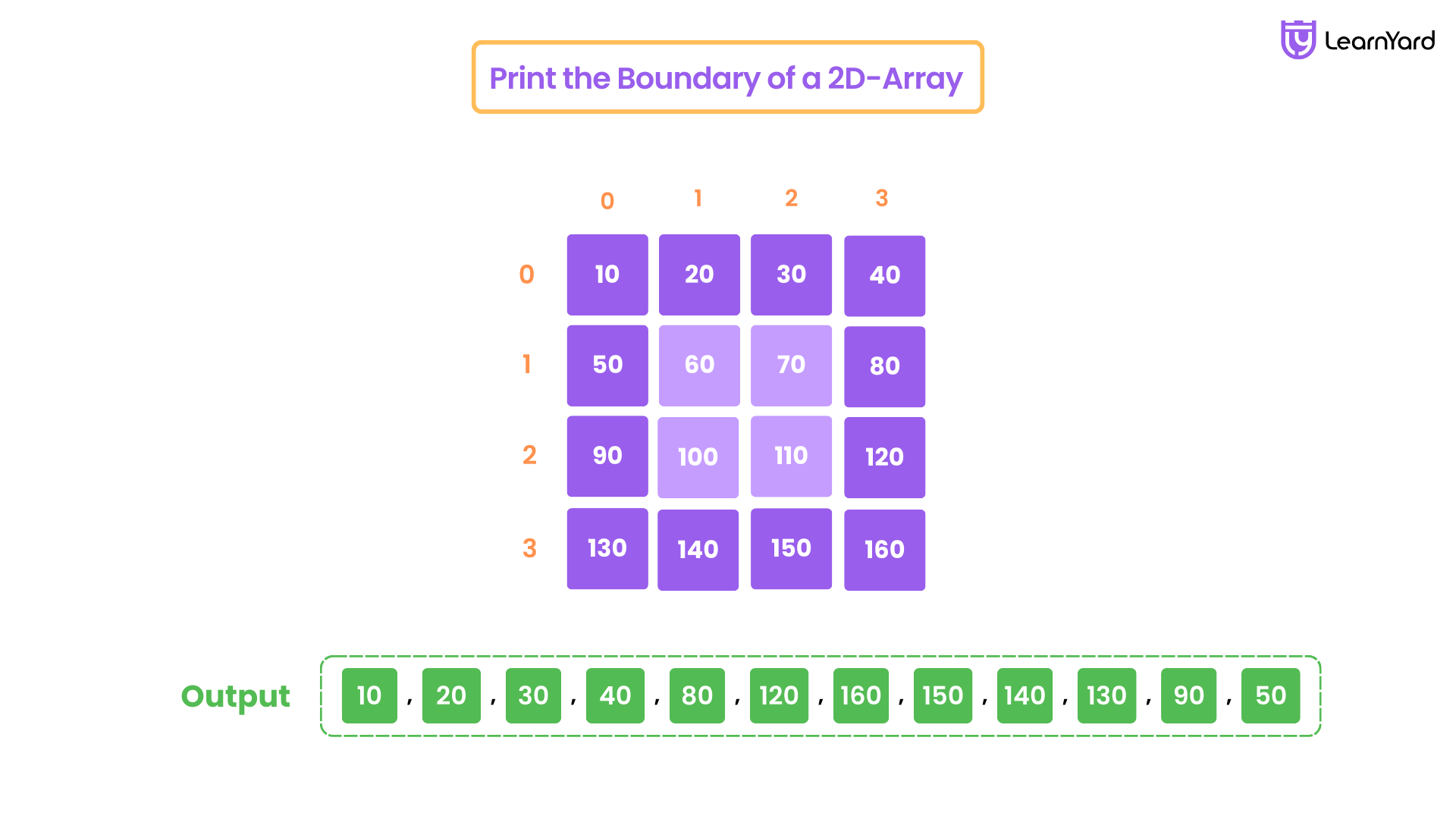
int[][] mat = { {10, 20, 30, 40}, {50, 60, 70, 80}, {90, 100, 110, 120}, {130, 140, 150, 160} };
Output
10 20 30 40 80 120 160 150 140 130 90 50
Intuition
Imagine you have a 2D array (or a matrix) which is essentially a grid made up of rows and columns. Our goal is to print the boundary (outermost edge) elements of this grid, starting from the top-left corner and moving around the edges in a clockwise direction.
Think of the grid as a picture frame: The "boundary" is simply the frame around the grid. So, imagine peeling off the outer frame of the picture and laying it out in a line. This is what we need to print.
What are boundary elements ?
The boundary elements are those that are located on the outermost rows and columns.
What are we printing ?We will print:
The first row (from left to right).
The last column (from top to bottom, excluding the first row).
The last row (from right to left, excluding the last column).
The first column (from bottom to top, excluding the last row and first element of the first column).
In the above example, the boundary elements are :-
10, 20, 30, 40 (first row)
80, 120, 160 (last column)
150, 140, 130 (last row)
90, 50 (first column)
Steps by step breakdown
To print the boundary: Start with the top row: Print all elements from left to right.
Then, print the right column: For each row (except the first one, as we’ve already printed that element), print the element in the last column.
Then, print the bottom row: Print all elements in this row from right to left, excluding the element that has already been printed in the last column.
Finally, print the left column: Print all elements in the leftmost column (excluding the already printed elements at the corners).
Approach
Print the first row from left to right:
- Loop i from 0 to n-1.
- Print matrix[0][i] (elements of the first row).
Print the last column from top to bottom (excluding the first row):
- Loop i from 1 to n-1.
- Print matrix[i][n-1] (elements of the last column).
Print the last row from right to left (excluding the last column):
- Loop i from n-2 down to 0.
- Print matrix[n-1][i] (elements of the last row).
Print the first column from bottom to top (excluding the first and last rows):
- Loop i from n-2 down to 1.
- Print matrix[i][0] (elements of the first column).
Dry-Run
Step 1: Print the first row from left to right
Loop: For i = 0 to n-1 (i.e., from 0 to 3):
- i = 0: Print matrix[0][0] = 10.
- i = 1: Print matrix[0][1] = 20.
- i = 2: Print matrix[0][2] = 30.
- i = 3: Print matrix[0][3] = 40.
Output so far: 10 20 30 40
Step 2: Print the last column from top to bottom (excluding the first row)
Loop: For i = 1 to n-1 (i.e., from 1 to 3):
- i = 1: Print matrix[1][3] = 80.
- i = 2: Print matrix[2][3] = 120.
- i = 3: Print matrix[3][3] = 160.
Output so far: 10 20 30 40 80 120 160
Step 3: Print the last row from right to left (excluding the last column)
Loop: For i = n-2 down to 0 (i.e., from 2 to 0):
- i = 2: Print matrix[3][2] = 150.
- i = 1: Print matrix[3][1] = 140.
- i = 0: Print matrix[3][0] = 130.
Output so far: 10 20 30 40 80 120 160 150 140 130
Step 4: Print the first column from bottom to top (excluding the first and last rows)
Loop: For i = n-2 down to 1 (i.e., from 2 to 1):
- i = 2: Print matrix[2][0] = 90.
- i = 1: Print matrix[1][0] = 50.
Output 10 20 30 40 80 120 160 150 140 130 90 50
Code in all Languages
1. C++ Try on Compiler
#include <iostream>
#include <vector>
using namespace std;
// Function to print the boundary of the matrix
void printBoundary(const vector<vector<int>>& mat, int n) {
// Print the first row
for (int i = 0; i < n; i++) {
cout << mat[0][i] << " ";
}
// Print the last column (excluding the first row)
for (int i = 1; i < n; i++) {
cout << mat[i][n-1] << " ";
}
// Print the last row (excluding the last column)
for (int i = n-2; i >= 0; i--) {
cout << mat[n-1][i] << " ";
}
// Print the first column (excluding the first and last rows)
for (int i = n-2; i > 0; i--) {
cout << mat[i][0] << " ";
}
}
int main() {
int n;
cout << "Enter the size of the matrix (n): ";
cin >> n;
vector<vector<int>> mat(n, vector<int>(n));
cout << "Enter the elements of the matrix:" << endl;
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> mat[i][j];
}
}
cout << "Boundary elements: ";
printBoundary(mat, n);
return 0;
}
2. Java Try on Compiler
import java.util.Scanner;
public class Main {
// Function to print the boundary of the matrix
public static void printBoundary(int[][] mat, int n) {
// Print the first row
for (int i = 0; i < n; i++) {
System.out.print(mat[0][i] + " ");
}
// Print the last column (excluding the first row)
for (int i = 1; i < n; i++) {
System.out.print(mat[i][n - 1] + " ");
}
// Print the last row (excluding the last column)
for (int i = n - 2; i >= 0; i--) {
System.out.print(mat[n - 1][i] + " ");
}
// Print the first column (excluding the first and last rows)
for (int i = n - 2; i > 0; i--) {
System.out.print(mat[i][0] + " ");
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
System.out.print("Enter the size of the matrix (n): ");
int n = sc.nextInt();
// Create a matrix of size n x n
int[][] mat = new int[n][n];
System.out.println("Enter the elements of the matrix:");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
mat[i][j] = sc.nextInt();
}
}
System.out.println("Boundary elements:");
printBoundary(mat, n);
sc.close();
}
}
3. Python Try on Compiler
def print_boundary(mat, n):
# Print the first row
for i in range(n):
print(mat[0][i], end=" ")
# Print the last column (excluding the first row)
for i in range(1, n):
print(mat[i][n-1], end=" ")
# Print the last row (excluding the last column)
for i in range(n-2, -1, -1):
print(mat[n-1][i], end=" ")
# Print the first column (excluding the first and last rows)
for i in range(n-2, 0, -1):
print(mat[i][0], end=" ")
def main():
n = int(input("Enter the size of the matrix (n): "))
mat = []
print("Enter the elements of the matrix:")
for i in range(n):
row = list(map(int, input().split()))
mat.append(row)
print("Boundary elements:")
print_boundary(mat, n)
if __name__ == "__main__":
main()
4. JavaScript Try on Compiler
const readline = require("readline-sync");
function printBoundary(mat, n) {
// Print the first row
for (let i = 0; i < n; i++) {
process.stdout.write(mat[0][i] + " ");
}
// Print the last column (excluding the first row)
for (let i = 1; i < n; i++) {
process.stdout.write(mat[i][n - 1] + " ");
}
// Print the last row (excluding the last column)
for (let i = n - 2; i >= 0; i--) {
process.stdout.write(mat[n - 1][i] + " ");
}
// Print the first column (excluding the first and last rows)
for (let i = n - 2; i > 0; i--) {
process.stdout.write(mat[i][0] + " ");
}
console.log(); // Add a newline after printing the boundary elements
}
function main() {
let n = parseInt(readline.question("Enter the size of the matrix (n): "));
let mat = [];
console.log("Enter the elements of the matrix:");
// Read matrix elements
for (let i = 0; i < n; i++) {
let row = readline.question(`Enter row ${i + 1}: `).split(" ").map(Number);
mat.push(row);
}
console.log("Boundary elements:");
printBoundary(mat, n);
}
// Call main function
main();
Time Complexity: O(n)
Time complexity is the total amount of time taken by the algorithm as a function of the input size.
- First row: We loop through n elements, so this takes O(n).
- Last column (excluding the first row): We loop through n−1 elements, so this takes O(n).
- Last row (excluding the last column): We loop through n−1 elements, so this takes O(n).
- First column (excluding the first and last rows): We loop through n−2 elements, so this takes O(n).
Overall, the total time complexity is: O(n)+O(n)+O(n)+O(n)=O(4n)=O(n)
Thus, Time Complexity = O(n), where n is the dimension of the matrix (number of rows or columns).
Space Complexity: O(1)
Auxiliary space complexity refers to the extra space or memory used by the algorithm, excluding the space used by the input.
- No additional data structures are used in the algorithm other than the input matrix itself. We only use a few variables for iteration (e.g., index variables like i in the loops).
- Thus, Auxiliary Space Complexity = O(1), since we are not using any extra space that grows with the size of the input.
Total Space Complexity
Total space complexity includes the space required for both the input and any additional space used by the algorithm.
- The input matrix is a 2D array of size n×n, so the space used by the matrix is O(n^2).
- The space for the iteration variables and print output is O(1).
Thus, Total Space Complexity = O(n^2), since the dominant space usage comes from the matrix itself.
We have learnt how to pint the boundary of a matrix. What if we are asked about a different way to traverse the 2D-Array ? What different way? Let's discuss on how we can traverse the 2D-Array in zig-zag fashion !!
Q12. Print Zig-Zag Matrix
Problem Desription
A zig-zag traversal of a 2D matrix involves traversing the matrix in a "zig-zag" pattern:
- Start from the top-left corner.
- Move diagonally upwards until you hit a boundary (top row or left column).
- Switch direction and move diagonally downwards until you hit a boundary (bottom row or right column).
- Repeat this process until every element is traversed.
Example
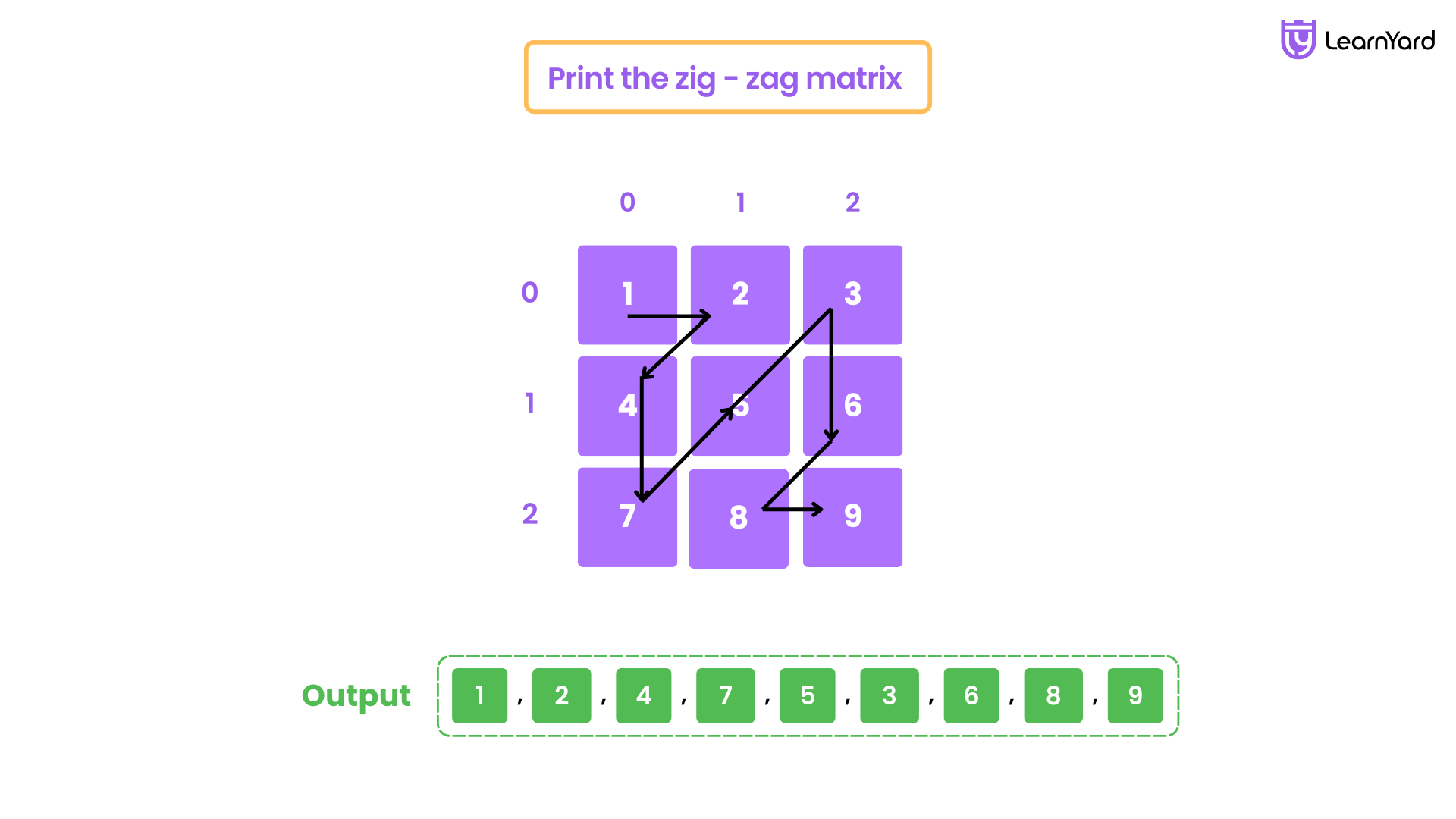
Input: mat[][]= {{1 2 3},{4 5 6},{7 8 9}}
Output: 1, 2, 4, 7, 5, 3, 6, 8, 9
Intuition
To code this, you need to understand the pattern of movement. Let's break it into simpler steps:
There are two main directions:
Upwards diagonal: Moving diagonally up and to the right.
Downwards diagonal: Moving diagonally down and to the left.
What will happen when we hit a boundary hit cell while moving through the directions ?
If we're moving upwards and hit the top row, we can’t go higher! You must switch to moving downwards.
Similarly, if you're moving downwards and hit the bottom row, you must switch to moving upwards.
What if we encounter few of the corner-cases ?
What if we're at the top row (row = 0) but not at the last column? We will move right.
Likewise, if you're at the last column but not the bottom row, we will move down.
If we're at the bottom row but not the first column,we will move right.
If you're at the first column, move down.
We have to follow the above cases until we completely done with our traversal.
Approach
Initialize variables: result = [] to store the zig-zag order ,
row = 0, col = 0 to track your position in the matrix.
upwards = true to represent the starting direction.
While the position (row, col) is within bounds of the matrix: Add the current element matrix[row][col] to result.
If moving upwards:
- If you're at the top row (row = 0) but not the last column: Move right (col++), and switch direction (upwards = false).
- If you're at the last column: Move down (row++), and switch direction (upwards = false).
- Otherwise: Move diagonally up (row--, col++).
If moving downwards:
- If you're at the bottom row but not the last column: Move right (col++), and switch direction (upwards = true).
- If you're at the first column: Move down (row++), and switch direction (upwards = true).
- Otherwise: Move diagonally down (row++, col--).
Repeat this process until row or col exceeds the boundaries of the matrix.
Return result.
Dry-Run
Initial State
- Result: [] (empty list to store the zig-zag traversal)
- Position: row = 0, col = 0 (starting at the top-left corner)
- Direction: upwards = true (initially moving upwards diagonally)
Dry-Run Steps
Step 1: Start at (0, 0)
Add mat[0][0] = 1 to result. Result: [1]
Moving upwards diagonally:
- Hit the top row (row = 0), so move right to (0, 1), and change direction to downwards.
- Position: row = 0, col = 1
- Direction: upwards = false
Step 2: Now at (0, 1):
Add mat[0][1] = 2 to result.Result: [1, 2]
Moving downwards diagonally:
- Move to (1, 0) (down-left).
- Position: row = 1, col = 0
- Direction: upwards = false
Step 3: Now at (1, 0)
Add mat[1][0] = 4 to result. Result: [1, 2, 4]
Moving downwards diagonally:
- Hit the first column (col = 0), so move down to (2, 0), and change direction to upwards.
- Position: row = 2, col = 0
- Direction: upwards = true
Step 4: Now at (2, 0)
Add mat[2][0] = 7 to result. Result: [1, 2, 4, 7]
Moving upwards diagonally:
- Move to (1, 1) (up-right).
- Position: row = 1, col = 1
- Direction: upwards = true
Step 5: Now at (1, 1)
Add mat[1][1] = 5 to result. Result: [1, 2, 4, 7, 5]
Moving upwards diagonally:
- Move to (0, 2) (up-right).
- Position: row = 0, col = 2
- Direction: upwards = true
Step 6: Now at (0, 2)
Add mat[0][2] = 3 to result. Result: [1, 2, 4, 7, 5, 3]
Moving upwards diagonally:
- Hit the last column (col = 2), so move down to (1, 2), and change direction to downwards.
- Position: row = 1, col = 2
- Direction: upwards = false
Step 7: Now at (1, 2)
Add mat[1][2] = 6 to result. Result: [1, 2, 4, 7, 5, 3, 6]
Moving downwards diagonally:
- Move to (2, 1) (down-left).
- Position: row = 2, col = 1
- Direction: upwards = false
Step 8: Now at (2, 1)
Add mat[2][1] = 8 to result. Result: [1, 2, 4, 7, 5, 3, 6, 8]
Moving downwards diagonally:
- Hit the bottom row (row = 2), so move right to (2, 2), and change direction to upwards.
- Position: row = 2, col = 2
- Direction: upwards = true
Step 9: Now at (2, 2)
Add mat[2][2] = 9 to result. Result: [1, 2, 4, 7, 5, 3, 6, 8, 9]
Moving upwards diagonally: Hit the last column and bottom row; traversal ends.
Final Result: [1, 2, 4, 7, 5, 3, 6, 8, 9]
Code in all Languages
1. C++ Try on Compiler
#include <iostream>
#include <vector>
using namespace std;
// Function to perform Zig-Zag traversal
vector<int> zigzagTraversal(vector<vector<int>> &matrix) {
// Get the dimensions of the matrix
int rows = matrix.size();
int cols = matrix[0].size();
// Result vector to store the traversal order
vector<int> result;
// Initialize the starting position and direction
int row = 0, col = 0;
bool upwards = true;
// Traverse until all elements are visited
while (row < rows && col < cols) {
// Add the current element to the result
result.push_back(matrix[row][col]);
// Handle the direction of movement
if (upwards) {
// Move diagonally up
if (row == 0 && col < cols - 1) {
col++; // Hit the top row, move right
upwards = false;
} else if (col == cols - 1) {
row++; // Hit the last column, move down
upwards = false;
} else {
row--; // Move diagonally up
col++;
}
} else {
// Move diagonally down
if (col == 0 && row < rows - 1) {
row++; // Hit the first column, move down
upwards = true;
} else if (row == rows - 1) {
col++; // Hit the bottom row, move right
upwards = true;
} else {
row++; // Move diagonally down
col--;
}
}
}
// Return the zig-zag order
return result;
}
int main() {
// Input number of rows and columns
int rows, cols;
cout << "Enter the number of rows and columns: ";
cin >> rows >> cols;
// Input the matrix elements
vector<vector<int>> matrix(rows, vector<int>(cols));
cout << "Enter the matrix elements:\n";
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
cin >> matrix[i][j];
}
}
// Perform Zig-Zag traversal
vector<int> result = zigzagTraversal(matrix);
// Output the result
cout << "Zig-Zag Traversal: ";
for (int num : result) {
cout << num << " ";
}
cout << endl;
return 0;
}
2. Java Try on Compiler
import java.util.Scanner;
import java.util.ArrayList;
public class ZigZagMatrix {
// Function to perform Zig-Zag traversal
public static ArrayList<Integer> zigzagTraversal(int[][] matrix) {
// Get the dimensions of the matrix
int rows = matrix.length;
int cols = matrix[0].length;
// Result list to store the traversal order
ArrayList<Integer> result = new ArrayList<>();
// Initialize the starting position and direction
int row = 0, col = 0;
boolean upwards = true;
// Traverse until all elements are visited
while (row < rows && col < cols) {
// Add the current element to the result
result.add(matrix[row][col]);
// Handle the direction of movement
if (upwards) {
// Move diagonally up
if (row == 0 && col < cols - 1) {
col++; // Hit the top row, move right
upwards = false;
} else if (col == cols - 1) {
row++; // Hit the last column, move down
upwards = false;
} else {
row--; // Move diagonally up
col++;
}
} else {
// Move diagonally down
if (col == 0 && row < rows - 1) {
row++; // Hit the first column, move down
upwards = true;
} else if (row == rows - 1) {
col++; // Hit the bottom row, move right
upwards = true;
} else {
row++; // Move diagonally down
col--;
}
}
}
// Return the zig-zag order
return result;
}
public static void main(String[] args) {
// Input number of rows and columns
Scanner sc = new Scanner(System.in);
System.out.print("Enter the number of rows and columns: ");
int rows = sc.nextInt();
int cols = sc.nextInt();
// Input the matrix elements
int[][] matrix = new int[rows][cols];
System.out.println("Enter the matrix elements:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
matrix[i][j] = sc.nextInt();
}
}
// Perform Zig-Zag traversal
ArrayList<Integer> result = zigzagTraversal(matrix);
// Output the result
System.out.println("Zig-Zag Traversal: " + result);
}
}
3. Python Try on Compiler
def zigzag_traversal(matrix):
# Get the dimensions of the matrix
rows = len(matrix)
cols = len(matrix[0])
# Result list to store the traversal order
result = []
# Initialize the starting position and direction
row, col = 0, 0
upwards = True
# Traverse until all elements are visited
while row < rows and col < cols:
# Add the current element to the result
result.append(matrix[row][col])
# Handle the direction of movement
if upwards:
# Move diagonally up
if row == 0 and col < cols - 1:
col += 1 # Hit the top row, move right
upwards = False
elif col == cols - 1:
row += 1 # Hit the last column, move down
upwards = False
else:
row -= 1 # Move diagonally up
col += 1
else:
# Move diagonally down
if col == 0 and row < rows - 1:
row += 1 # Hit the first column, move down
upwards = True
elif row == rows - 1:
col += 1 # Hit the bottom row, move right
upwards = True
else:
row += 1 # Move diagonally down
col -= 1
# Return the zig-zag order
return result
# Input number of rows and columns
rows, cols = map(int, input("Enter the number of rows and columns: ").split())
# Input the matrix elements
matrix = []
print("Enter the matrix elements:")
for _ in range(rows):
matrix.append(list(map(int, input().split())))
# Perform Zig-Zag traversal
result = zigzag_traversal(matrix)
# Output the result
print("Zig-Zag Traversal:", result)
4. JavaScript Try on Compiler
const readline = require("readline-sync");
function zigzagTraversal(matrix) {
// Get the dimensions of the matrix
const rows = matrix.length;
const cols = matrix[0].length;
// Result array to store the traversal order
const result = [];
// Initialize the starting position and direction
let row = 0, col = 0;
let upwards = true;
// Traverse until all elements are visited
while (row < rows && col < cols) {
// Add the current element to the result
result.push(matrix[row][col]);
// Handle the direction of movement
if (upwards) {
// Move diagonally up
if (row === 0 && col < cols - 1) {
col++; // Hit the top row, move right
upwards = false;
} else if (col === cols - 1) {
row++; // Hit the last column, move down
upwards = false;
} else {
row--; // Move diagonally up
col++;
}
} else {
// Move diagonally down
if (col === 0 && row < rows - 1) {
row++; // Hit the first column, move down
upwards = true;
} else if (row === rows - 1) {
col++; // Hit the bottom row, move right
upwards = true;
} else {
row++; // Move diagonally down
col--;
}
}
}
// Return the zig-zag order
return result;
}
// Input the number of rows and columns
const rows = parseInt(readline.question("Enter the number of rows: "));
const cols = parseInt(readline.question("Enter the number of columns: "));
// Input the matrix elements
const matrix = [];
for (let i = 0; i < rows; i++) {
const row = readline.question(`Enter row ${i + 1} (space-separated): `).split(" ").map(Number);
matrix.push(row);
}
// Perform Zig-Zag traversal
const result = zigzagTraversal(matrix);
// Output the result
console.log("Zig-Zag Traversal:", result);
Time Complexity: O(rows x cols)
Let the dimensions of the matrix be rows (number of rows) and cols (number of columns).
Traversal of the matrix:
- The algorithm traverses each element of the matrix exactly once.
- This means there are a total of rows×cols elements.
- Therefore, the time complexity for traversal is O(rows × cols).
Adding elements to the result:
- Each element is added to the result list/array during the traversal.
- Adding an element to the result is an O(1) operation.
- This operation is repeated rows×cols times.
- Hence, the overall time complexity remains O(rows × cols).
Space Complexity: O(rows x cols)
Result array/list:
- We use an array or list to store the result.
- The result will contain rows×colsrows \times colsrows×cols elements.
- This requires O(rows × cols) space.
Auxiliary variables:
- We use a few integer variables (row, col, upwards) to manage the traversal.
- These require O(1) space.
Matrix: The input matrix is not duplicated or modified, so it does not contribute additional space complexity.
Thus, the overall space complexity is O(rows × cols) due to the storage of the result.
Since, we have learnt the ways to traverse a 2D-Array, now it is important for us to learn about the diversity of 2D-Arrays. Diversity of 2D-Arrays? There are different types of 2D-Arrays based on the values it has and how it can be used to solve real-world problems. In the next few articles, we will learn about them.
Q13. Symmetric Matrix
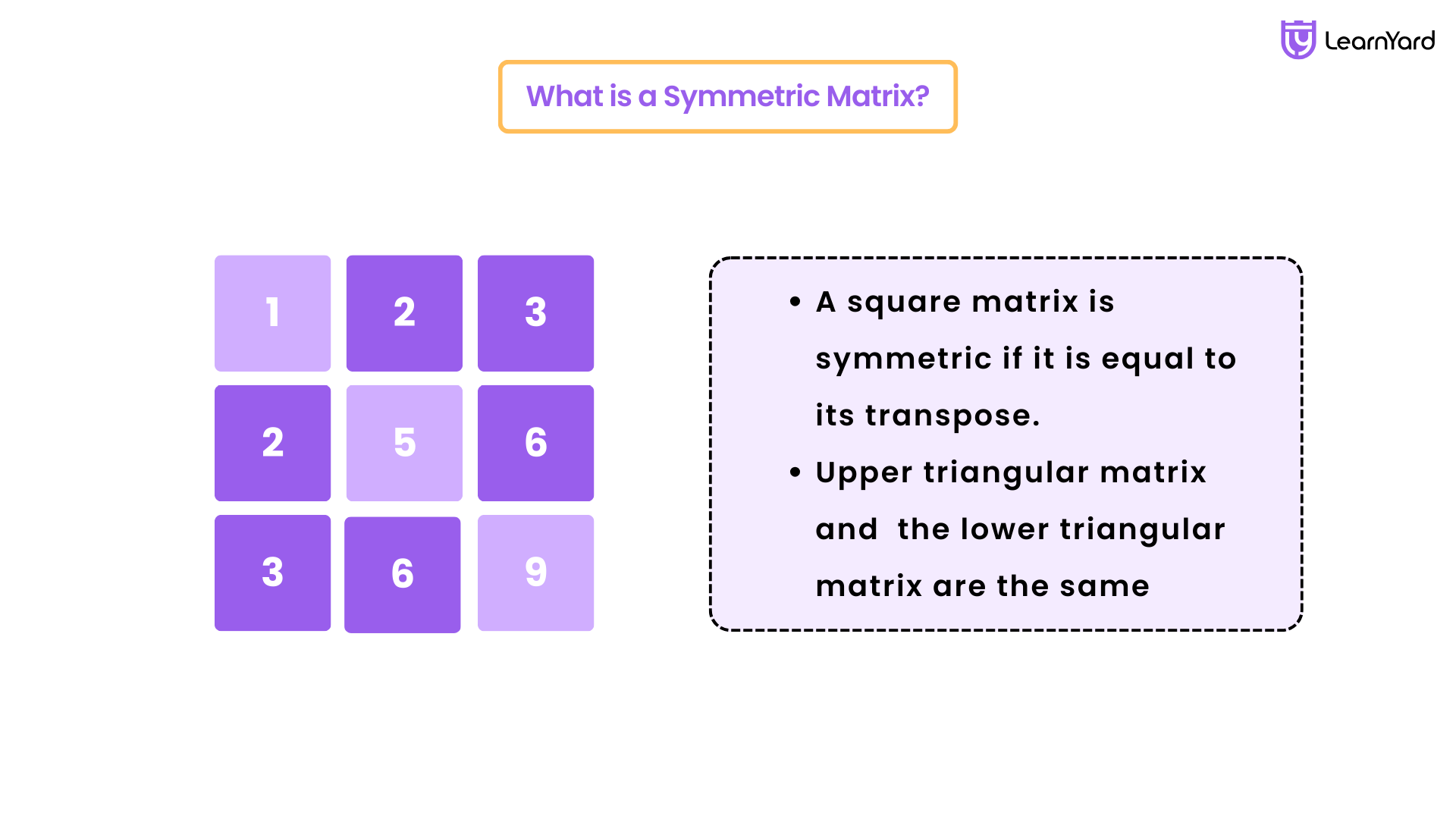
A square matrix is symmetric if it is equal to its transpose.
What is the transpose of a matrix?
The transpose of a matrix is obtained by flipping the matrix over its diagonal. In other words, the rows of the original matrix become the columns in the transposed matrix, and the columns become the rows.
If the original matrix is A with dimensions m×n, the transposed matrix AT will have dimensions n×m, and: AT[i][j]=A[j][i]
For example if
A[][]= {{ 1, 2, 3 },
{ 4, 5, 6 }}
AT[][]= {{1, 4},
{2, 5},
{3, 6}}
Example
Input:
mat[][] ={{ 1, 2, 3 },{ 2, 5, 6 },{ 3, 6, 9 }}
Output: Yes, it is symmetric.
Intuition
We are tasked to check whether a given square matrix is symmetric. If it is not a square matrix, we can immediately say it is not symmetric.
How do we check symmetry ?
First, we’ll confirm the matrix is square n×n. Next, we’ll focus on the upper triangular part of the matrix (above the diagonal) and check if it mirrors the lower triangular part (below the diagonal).
- For any position (i,j), we’ll compare matrix[i][j] with matrix[j][i] .
- If they differ for any pair, the matrix is not symmetric.
By focusing on this diagonal symmetry, we can avoid extra calculations and make the process efficient.
Approach
Outer Loop: Start with the row index iii.
- Loop through i=0 to n−1, where n is the size of the square matrix.
- This loop ensures we check each row of the matrix.
Inner Loop: For each row index i, loop through the column index j starting from i+1 to n−1. Why j=i+1? Because we’re only interested in the upper triangular part of the matrix (above the diagonal).
Compare Elements:
- At each iteration, compare matrix[i][j] (upper triangular element) with matrix[j][i] (corresponding lower triangular element).
- If matrix[i][j]≠matrix[j][i], this means the matrix is not symmetric, and we return "Not symmetric".
Continue the Loops: If all elements in the upper triangular part match their corresponding elements in the lower triangular part, the matrix is symmetric.
Return Result: If no mismatches are found, return "Symmetric".
Dry-Run
Input:
mat[][] =
{{ 1, 2, 3 },
{ 2, 5, 6 },
{ 3, 6, 9 }}
Output: Yes, it is symmetric.
Dry-Run the steps
- We check matrix[0][1] against matrix[1][0] . Both are 2, so it’s fine.
- We check matrix[0][2] against matrix[2][0]. Both are 3, so it’s fine.
- We check matrix[1][2] against matrix[2][1]. Both are 6, so it’s fine.
Since all the elements match their symmetric counterparts, the matrix is symmetric.
Code in all Languages
1. C++ Try on Compiler
#include <iostream>
#include <vector>
using namespace std;
// Function to check if a matrix is symmetric
bool isSymmetric(vector<vector<int>> &matrix) {
// Get the size of the matrix
int n = matrix.size();
// Loop through the upper triangular part
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// Check if elements are symmetric
if (matrix[i][j] != matrix[j][i]) {
return false; // Not symmetric
}
}
}
// If all elements match, it is symmetric
return true;
}
int main() {
int n;
cout << "Enter the size of the square matrix: ";
cin >> n;
// Input the matrix
vector<vector<int>> matrix(n, vector<int>(n));
cout << "Enter the matrix elements row by row:\n";
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> matrix[i][j];
}
}
// Check symmetry
if (isSymmetric(matrix)) {
cout << "Yes, the matrix is symmetric.\n";
} else {
cout << "No, the matrix is not symmetric.\n";
}
return 0;
}
2. Java Try on Compiler
import java.util.Scanner;
public class SymmetricMatrix {
// Function to check if a matrix is symmetric
public static boolean isSymmetric(int[][] matrix) {
int n = matrix.length;
// Loop through the upper triangular part
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// Check if elements are symmetric
if (matrix[i][j] != matrix[j][i]) {
return false; // Not symmetric
}
}
}
return true; // Symmetric
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
// Input the size of the square matrix
System.out.print("Enter the size of the square matrix: ");
int n = sc.nextInt();
// Input the matrix elements
int[][] matrix = new int[n][n];
System.out.println("Enter the matrix elements row by row:");
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
matrix[i][j] = sc.nextInt();
}
}
// Check symmetry
if (isSymmetric(matrix)) {
System.out.println("Yes, the matrix is symmetric.");
} else {
System.out.println("No, the matrix is not symmetric.");
}
sc.close();
}
}3. Python Try on Compiler
def is_symmetric(matrix):
n = len(matrix)
# Loop through the upper triangular part
for i in range(n):
for j in range(i + 1, n):
# Check if elements are symmetric
if matrix[i][j] != matrix[j][i]:
return False # Not symmetric
return True # Symmetric
# Input the size of the square matrix
n = int(input("Enter the size of the square matrix: "))
# Input the matrix elements
matrix = []
print("Enter the matrix elements row by row:")
for _ in range(n):
row = list(map(int, input().split()))
matrix.append(row)
# Check symmetry
if is_symmetric(matrix):
print("Yes, the matrix is symmetric.")
else:
print("No, the matrix is not symmetric.")
4. JavaScript Try on Compiler
const readline = require('readline');
// Create a readline interface for input/output
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
// Function to check if a matrix is symmetric
function isSymmetric(matrix) {
const n = matrix.length;
// Loop through the upper triangular part
for (let i = 0; i < n; i++) {
for (let j = i + 1; j < n; j++) {
// Check if elements are symmetric
if (matrix[i][j] !== matrix[j][i]) {
return false; // Not symmetric
}
}
}
return true; // Symmetric
}
// Main function to handle user input
const main = () => {
rl.question("Enter the size of the square matrix: ", (nInput) => {
const n = parseInt(nInput); // Size of the matrix
const matrix = [];
console.log("Enter the matrix elements row by row:");
let rowIndex = 0;
const readRow = () => {
if (rowIndex < n) {
rl.question(`Row ${rowIndex + 1}: `, (row) => {
matrix.push(row.split(" ").map(Number)); // Parse the row as integers
rowIndex++;
readRow(); // Read the next row
});
} else {
// All rows are input, check symmetry
if (isSymmetric(matrix)) {
console.log("Yes, the matrix is symmetric.");
} else {
console.log("No, the matrix is not symmetric.");
}
rl.close(); // Close the readline interface
}
};
readRow(); // Start reading rows
});
};
// Call the main function
main();
Time Complexity: O(n²)
We compare only the upper triangular part of the matrix with its lower triangular counterpart.
The number of comparisons is n(n−1)/2 , which simplifies to O(n²).
Overall Time Complexity: The total time complexity is: O(n²) + O(n²) = O(n²).
Space Complexity: O(1)
Auxiliary Space Complexity
Auxiliary space refers to the extra memory used during execution (excluding input storage):
Symmetry Check:The comparison loop does not use additional space apart from a few counters (constant space).
Auxiliary Space Complexity: O(1)
Total Space Complexity
Space complexity accounts for all memory used:
Matrix Storage: The program explicitly stores the n×n matrix in memory. Space required for this is O(n²).
Total Space Complexity is O(1) + O(n²) = O(n²).