2D- Arrays II
As we have learnt the two types of traversal techniques that we can perform in a matrix. Now, it's very important for us to apply those in questions. Before , moving further we must make sure we are perfect with the row-wise and the column wise traversals.
Q6. Maximum and Minimum element of each Row
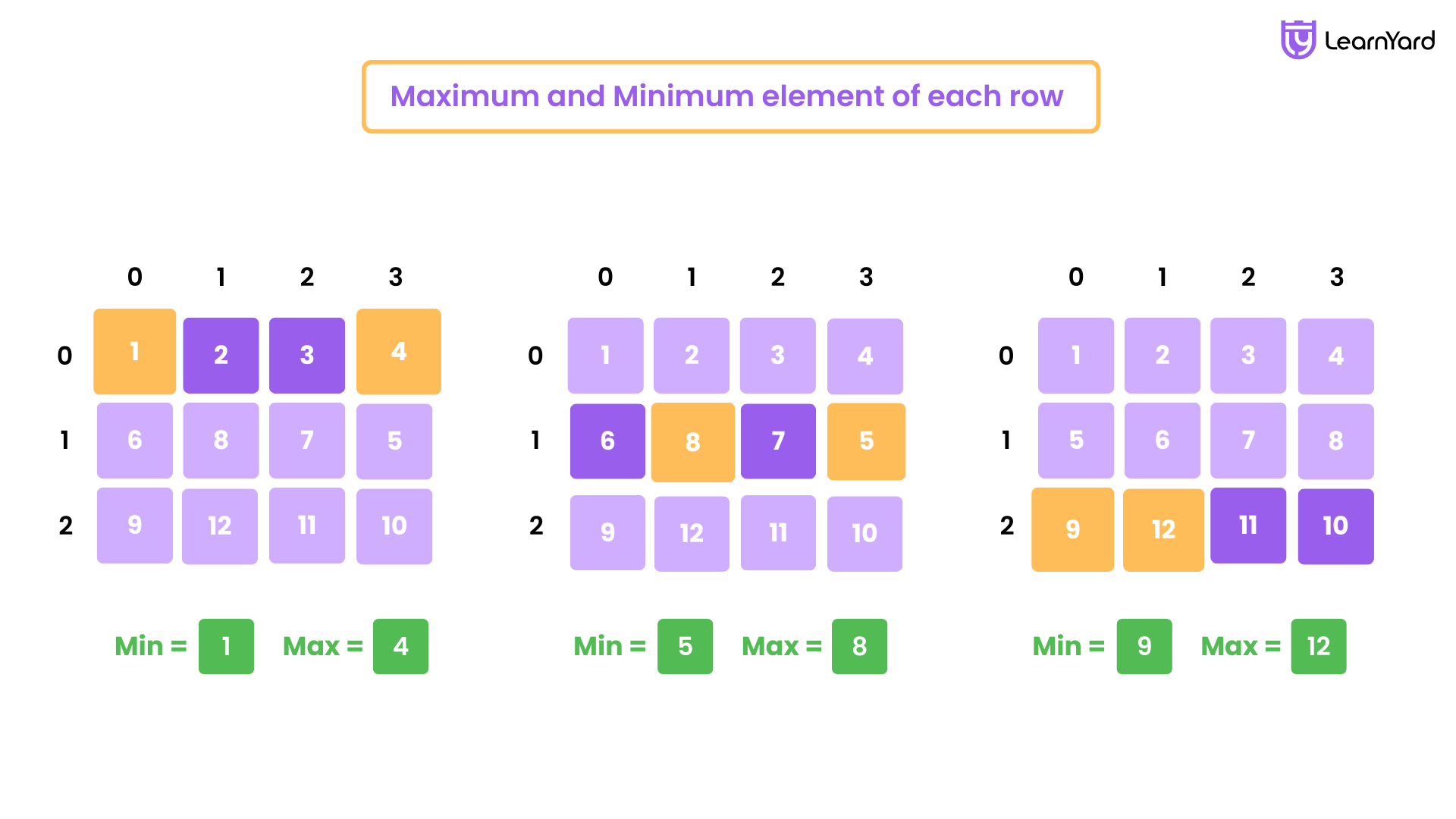
Example
Input : mat[][] = {{1, 2, 3,4}, {6,8,7,5}, {9,12,11,10}}
Output : Max of row 1: 4, Min of row 1 : 1
Max of row 2: 8, Min of col2 : 5
Max of row 3: 12, Min of col3 :9
Intuition
We are given a 2D-array/matrix of size M x N. We are asked to find the minimum and maximum element of each row of the given matrix.
Since, we are aware of row wise traversal of a 2D array. We just need to traverse each array of the 2D array/matrix . Each time we encounter an element we will compare the value with the min and max values and then print the maximum and minimum value of each row.
Approach
Loop Through Each Row: We use an outer loop to iterate through each row of the matrix. The loop runs from i=0 to i=mat.length .
Initialize Maximum and Minimum Values for Each Row: For each row, initialize two variables, max and min, to store the maximum and minimum elements of that row. We set max to the smallest possible value and min to the largest possible value to ensure that no values in the 2d-array can be smaller or larger than min and max.
Traverse the Row to Find Max and Min: We use an inner loop to iterate through each element of the row. We declare an inner loop from j=0 to j=mat[0].length.
For each element in the row: We will update max if the element is greater than the current value of max and will update min if the element is smaller than the current value of min.
Print the Results: After traversing all elements in the row, print the values of max and min for that row.
Dry-Run
Row 1: {1, 2, 3, 4}
Initialize max as Integer.MIN_VALUE and min as Integer.MAX_VALUE.
Traverse through the row:
First element 1: max = max(1, -∞) = 1 ,min = min(1, ∞) = 1
Second element 2: max = max(2, 1) = 2, min = min(2, 1) = 1
Third element 3: max = max(3, 2) = 3, min = min(3, 1) = 1
Fourth element 4: max = max(4, 3) = 4, min = min(4, 1) = 1
Result for Row 1: Max = 4, Min = 1
Output: "Max of row 1: 4, Min of row 1: 1"
Row 2: {6, 8, 7, 5}
Initialize max as Integer.MIN_VALUE and min as Integer.MAX_VALUE.
Traverse through the row:
First element 6: max = max(6, -∞) = 6, min = min(6, ∞) = 6
Second element 8: max = max(8, 6) = 8, min = min(8, 6) = 6
Third element 7: max = max(7, 8) = 8, min = min(7, 6) = 6
Fourth element 5: max = max(5, 8) = 8, min = min(5, 6) = 5
Result for Row 2: Max = 8, Min = 5
Output: "Max of row 2: 8, Min of row 2: 5"
Row 3: {9, 12, 11, 10}
Initialize max as Integer.MIN_VALUE and min as Integer.MAX_VALUE.
Traverse through the row:
First element 9: max = max(9, -∞) = 9, min = min(9, ∞) = 9
Second element 12: max = max(12, 9) = 12, min = min(12, 9) = 9
Third element 11: max = max(11, 12) = 12, min = min(11, 9) = 9
Fourth element 10: max = max(10, 12) = 12, min = min(10, 9) = 9
Result for Row 3: Max = 12, Min = 9
Output: "Max of row 3: 12, Min of row 3: 9"
Final Output
The program would output:
Max of row 1: 4, Min of row 1: 1
Max of row 2: 8, Min of row 2: 5
Max of row 3: 12, Min of row 3: 9
Code in all Languages
1. C++ Try on Compiler
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
// Function to calculate max and min of each row
void rowMaxMin(vector<vector<int>>& matrix) {
for (int i = 0; i < matrix.size(); i++) {
int maxVal = INT_MIN;
int minVal = INT_MAX;
// Traverse through each element of the current row
for (int j = 0; j < matrix[i].size(); j++) {
maxVal = max(maxVal, matrix[i][j]);
minVal = min(minVal, matrix[i][j]);
}
// Output max and min of the current row
cout << "Max of row " << i + 1 << ": " << maxVal << ", Min of row " << i + 1 << ": " << minVal << endl;
}
}
int main() {
int rows, cols;
// Take user input for matrix dimensions
cout << "Enter number of rows: ";
cin >> rows;
cout << "Enter number of columns: ";
cin >> cols;
vector<vector<int>> matrix(rows, vector<int>(cols));
// Populate matrix with user input
cout << "Enter matrix elements:" << endl;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
cin >> matrix[i][j];
}
}
// Calculate and display max and min for each row
rowMaxMin(matrix);
return 0;
}
2. Java Try on Compiler
import java.util.Scanner;
public class RowMaxMin {
// Function to calculate max and min of each row
static void rowMaxMin(int[][] matrix) {
for (int i = 0; i < matrix.length; i++) {
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
// Traverse through each element of the current row
for (int j = 0; j < matrix[i].length; j++) {
max = Math.max(max, matrix[i][j]);
min = Math.min(min, matrix[i][j]);
}
// Output max and min of the current row
System.out.println("Max of row " + (i + 1) + ": " + max + ", Min of row " + (i + 1) + ": " + min);
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// Take user input for matrix dimensions
System.out.print("Enter number of rows: ");
int rows = scanner.nextInt();
System.out.print("Enter number of columns: ");
int cols = scanner.nextInt();
// Initialize matrix
int[][] matrix = new int[rows][cols];
// Populate matrix with user input
System.out.println("Enter matrix elements:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
matrix[i][j] = scanner.nextInt();
}
}
// Calculate and display max and min for each row
rowMaxMin(matrix);
scanner.close();
}
}
3. Python Try on Compiler
# Function to calculate max and min of each row
def row_max_min(matrix):
for i in range(len(matrix)):
max_val = float('-inf')
min_val = float('inf')
# Traverse through each element of the current row
for j in range(len(matrix[i])):
max_val = max(max_val, matrix[i][j])
min_val = min(min_val, matrix[i][j])
# Output max and min of the current row
print(f"Max of row {i + 1}: {max_val}, Min of row {i + 1}: {min_val}")
# Take user input for matrix dimensions
rows = int(input("Enter number of rows: "))
cols = int(input("Enter number of columns: "))
# Populate matrix with user input
matrix = []
print("Enter matrix elements:")
for i in range(rows):
row = list(map(int, input().split()))
matrix.append(row)
# Calculate and display max and min for each row
row_max_min(matrix)
4. JavaScript Try on Compiler
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
// Function to calculate max and min of each row
function rowMaxMin(matrix) {
for (let i = 0; i < matrix.length; i++) {
let max = Number.NEGATIVE_INFINITY;
let min = Number.POSITIVE_INFINITY;
// Traverse through each element of the current row
for (let j = 0; j < matrix[i].length; j++) {
max = Math.max(max, matrix[i][j]);
min = Math.min(min, matrix[i][j]);
}
// Output max and min of the current row
console.log(`Max of row ${i + 1}: ${max}, Min of row ${i + 1}: ${min}`);
}
}
// Start user input for matrix dimensions
rl.question("Enter number of rows: ", (rowsInput) => {
rl.question("Enter number of columns: ", (colsInput) => {
const rows = parseInt(rowsInput);
const cols = parseInt(colsInput);
const matrix = [];
let rowCounter = 0;
console.log("Enter matrix elements:");
// Function to collect row input
function getRowInput() {
if (rowCounter < rows) {
rl.question(`Row ${rowCounter + 1}: `, (rowInput) => {
const row = rowInput.split(" ").map(Number);
matrix.push(row);
rowCounter++;
getRowInput(); // Recursively get the next row
});
} else {
// Once all rows are collected, calculate max and min
rowMaxMin(matrix);
rl.close(); // Close the readline interface
}
}
getRowInput(); // Start collecting rows
});
});
Time Complexity: O(n x m)
The algorithm uses a nested loop to iterate through each element in every row of the matrix:
Outer Loop: Iterates over each row — this runs m times, where m is the number of rows.
Inner Loop: Iterates over each element in the current row — this runs n times, where n is the number of columns.
Thus, the total time complexity is: O(n×m)
Space Complexity : O(n x m)
Auxiliary space refers to extra space used by the algorithm that is not part of the input.
The algorithm only uses a few fixed-size variables for storing the minimum and maximum values (min and max), as well as the loop counters. No additional space scales with the input size.
Therefore, the auxiliary space complexity is: O(1)
Total Space Complexity
Total space complexity accounts for both the input space and auxiliary space:
Input Matrix: The matrix itself occupies O(n×m) space.
Auxiliary Space: As calculated above, it is O(1).
Thus, the total space complexity is: O(n×m)
In the previous question, we got to know the application of row-wise traversal and understood the flow of it. Before moving to the next question, we have to make sure that we are clear with the column-wise traversal of a 2D-array/matrix.
Q7. Maximum and Minimum element of each Column

Example
Input : mat[][] = {{1, 2, 3,4}, {6,8,7,5}, {9,12,11,10}}
Output : Max of row 1: 4, Min of row 1 : 1
Max of row 2: 8, Min of col2 : 5
Max of row 3: 12, Min of col3 :9
Intuition
We are given a 2D-array/matrix of size M x N. We are asked to find the minimum and maximum element of each column of the given matrix.
Since, we are aware of column wise traversal of a 2D array.We just need to traverse each array of the 2D array/matrix .Each time we encounter an element we will compare the value with the min and max values and then print the maximum and minimum value of each column.
Approach
Loop Through Each Column: We use an outer loop to iterate through each column of the matrix.
Initialize Maximum and Minimum Values for Each Column: For each column, initialize two variables, max and min, to store the maximum and minimum elements of that column. Set max to the smallest possible value and min to the largest possible value .
Traverse the Column to Find Max and Min: Use an inner loop to iterate through each row, but keep the column index fixed, so you traverse the elements vertically.
For each element in the column: Update max if the current element is greater than the current value of max.
Update min if the current element is smaller than the current value of min.
Print the Results: After traversing all the rows for a particular column, print the values of max and min for that column.
Dry-Run
Column 1 (Index 0):
Traverse each row in column 1:
Row 1, Element: 1 → colMin = 1, colMax = 1
Row 2, Element: 6 → colMin = 1, colMax = 6
Row 3, Element: 9 → colMin = 1, colMax = 9
Result: Max of column 1 = 9, Min of column 1 = 1
Column 2 (Index 1):
Traverse each row in column 2:
Row 1, Element: 2 → colMin = 2, colMax = 2
Row 2, Element: 8 → colMin = 2, colMax = 8
Row 3, Element: 12 → colMin = 2, colMax = 12
Result: Max of column 2 = 12, Min of column 2 = 2
Column 3 (Index 2):
Traverse each row in column 3:
Row 1, Element: 3 → colMin = 3, colMax = 3
Row 2, Element: 7 → colMin = 3, colMax = 7
Row 3, Element: 11 → colMin = 3, colMax = 11
Result: Max of column 3 = 11, Min of column 3 = 3
Column 4 (Index 3):
Traverse each row in column 4:
Row 1, Element: 4 → colMin = 4, colMax = 4
Row 2, Element: 5 → colMin = 4, colMax = 5
Row 3, Element: 10 → colMin = 4, colMax = 10
Result: Max of column 4 = 10, Min of column 4 = 4
Max of column 1: 9, Min of column 1: 1
Max of column 2: 12, Min of column 2: 2
Max of column 3: 11, Min of column 3: 3
Max of column 4: 10, Min of column 4: 4
Code in all Languages
1. C++ Try on Compiler
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
// Function to calculate max and min of each column in the matrix
void columnMaxMin(const vector<vector<int>>& matrix) {
// Get the number of rows in the matrix
int rows = matrix.size();
// Get the number of columns in the matrix
int cols = matrix[0].size();
// Loop through each column
for (int j = 0; j < cols; j++) {
// Initialize minimum for the current column
int colMin = INT_MAX;
// Initialize maximum for the current column
int colMax = INT_MIN;
// Traverse each row in the current column
for (int i = 0; i < rows; i++) {
// Update column minimum if a smaller element is found
colMin = min(colMin, matrix[i][j]);
// Update column maximum if a larger element is found
colMax = max(colMax, matrix[i][j]);
}
// Display maximum and minimum for the current column (1-based index)
cout << "Max of column " << (j + 1) << ": " << colMax << ", Min of column " << (j + 1) << ": " << colMin << endl;
}
}
int main() {
int rows, cols;
// Prompt user for the number of rows in the matrix
cout << "Enter number of rows: ";
cin >> rows;
// Prompt user for the number of columns in the matrix
cout << "Enter number of columns: ";
cin >> cols;
// Initialize matrix with given dimensions
vector<vector<int>> matrix(rows, vector<int>(cols));
// Prompt user to enter matrix elements row by row
cout << "Enter matrix elements:" << endl;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
cin >> matrix[i][j];
}
}
// Call the function to calculate max and min of each column
columnMaxMin(matrix);
return 0;
}
2. Java Try on Compiler
import java.util.Scanner;
public class ColumnMaxMin {
// Function to calculate max and min of each column in the matrix
static void columnMaxMin(int[][] matrix) {
// Get the number of rows in the matrix
int rows = matrix.length;
// Get the number of columns in the matrix
int cols = matrix[0].length;
// Loop through each column
for (int j = 0; j < cols; j++) {
// Initialize minimum for the current column
int colMin = Integer.MAX_VALUE;
// Initialize maximum for the current column
int colMax = Integer.MIN_VALUE;
// Traverse each row in the current column
for (int i = 0; i < rows; i++) {
// Update column minimum if a smaller element is found
colMin = Math.min(colMin, matrix[i][j]);
// Update column maximum if a larger element is found
colMax = Math.max(colMax, matrix[i][j]);
}
// Display maximum and minimum for the current column (1-based index)
System.out.println("Max of column " + (j + 1) + ": " + colMax + ", Min of column " + (j + 1) + ": " + colMin);
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// Prompt user for the number of rows in the matrix
System.out.print("Enter number of rows: ");
int rows = scanner.nextInt();
// Prompt user for the number of columns in the matrix
System.out.print("Enter number of columns: ");
int cols = scanner.nextInt();
// Initialize the matrix with given dimensions
int[][] matrix = new int[rows][cols];
// Prompt user to enter matrix elements row by row
System.out.println("Enter matrix elements:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
matrix[i][j] = scanner.nextInt();
}
}
// Call the function to calculate max and min of each column
columnMaxMin(matrix);
// Close the scanner
scanner.close();
}
}
3. Python Try on Compiler
def column_max_min(matrix):
# Get the number of rows in the matrix
rows = len(matrix)
# Get the number of columns in the matrix
cols = len(matrix[0])
# Loop through each column
for j in range(cols):
# Initialize minimum for the current column
col_min = float('inf')
# Initialize maximum for the current column
col_max = float('-inf')
# Traverse each row in the current column
for i in range(rows):
# Update column minimum if a smaller element is found
col_min = min(col_min, matrix[i][j])
# Update column maximum if a larger element is found
col_max = max(col_max, matrix[i][j])
# Display maximum and minimum for the current column (1-based index)
print(f"Max of column {j + 1}: {col_max}, Min of column {j + 1}: {col_min}")
# Prompt user for the number of rows in the matrix
rows = int(input("Enter number of rows: "))
# Prompt user for the number of columns in the matrix
cols = int(input("Enter number of columns: "))
# Initialize the matrix with user-defined dimensions
matrix = []
print("Enter matrix elements:")
for i in range(rows):
row = list(map(int, input().split()))
matrix.append(row)
# Call the function to calculate max and min of each column
column_max_min(matrix)
4. JavaScript Try on Compiler
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
// Function to calculate max and min of each column
function columnMaxMin(matrix) {
// Get the number of rows in the matrix
let rows = matrix.length;
// Get the number of columns in the matrix
let cols = matrix[0].length;
// Loop through each column
for (let j = 0; j < cols; j++) {
// Initialize minimum for the current column
let colMin = Infinity;
// Initialize maximum for the current column
let colMax = -Infinity;
// Traverse each row in the current column
for (let i = 0; i < rows; i++) {
// Update column minimum if a smaller element is found
colMin = Math.min(colMin, matrix[i][j]);
// Update column maximum if a larger element is found
colMax = Math.max(colMax, matrix[i][j]);
}
// Display maximum and minimum for the current column (1-based index)
console.log(`Max of column ${j + 1}: ${colMax}, Min of column ${j + 1}: ${colMin}`);
}
}
// Prompt user for the number of rows and columns
rl.question("Enter number of rows: ", (rowsInput) => {
rl.question("Enter number of columns: ", (colsInput) => {
const rows = parseInt(rowsInput);
const cols = parseInt(colsInput);
const matrix = [];
let rowCounter = 0;
console.log("Enter matrix elements row by row:");
// Function to collect row input
function getRowInput() {
if (rowCounter < rows) {
rl.question(`Row ${rowCounter + 1}: `, (rowInput) => {
const row = rowInput.split(" ").map(Number);
matrix.push(row);
rowCounter++;
getRowInput(); // Recursively get the next row
});
} else {
// Once all rows are collected, calculate max and min for each column
columnMaxMin(matrix);
rl.close(); // Close the readline interface
}
}
getRowInput(); // Start collecting rows
});
});
Time Complexity: O(n x m)
Time Complexity
The algorithm uses two nested loops: an outer loop that iterates over each column (cols times) and an inner loop that iterates over each row (rows times).
Therefore, the total number of iterations is n * m.
Thus, Time Complexity = O(n * m).
Space Complexity: O(n x m)
Auxiliary Space Complexity
The algorithm only uses a constant amount of extra space to store variables (colMin and colMax) during each iteration.
No additional data structures are used based on the input size, so the Auxiliary Space Complexity = O(1).
Total Space Complexity
The total space complexity includes both the input matrix space and the auxiliary space.
Since the input matrix is n * m in size, the input space complexity is O(n * m).
Therefore, Total Space Complexity = O(n * m).
Since we have learned the row-wise traversal and column-wise traversal of a 2D Array/matrix. In the next few articles we will learn how we can manipulate matrices and implement our logic between two or more 2D-Arrays/matrix.
Q8. Add and subtract two matrix
Example
Input
matrix1[][] = {{1,2,3,4},{6,8,7,5},{9,12,11,10}}
matrix2[][] = {{7,3,2,1},{6,9,3,12},{9,23,24,11}}
Output: {{8,5,5,5},{12,17,10,17},{18,45,35,21}}
Intuition
We are given two 2D arrays of equal rows and column lengths.
We are asked to do arithmetic operations mainly addition and subtraction between the two matrices.
How can we perform those?
It's as simple as performing addition and subtraction between two numbers.
What we do is we perform:
Addition: Add each element in the first matrix to the corresponding element in the second matrix.
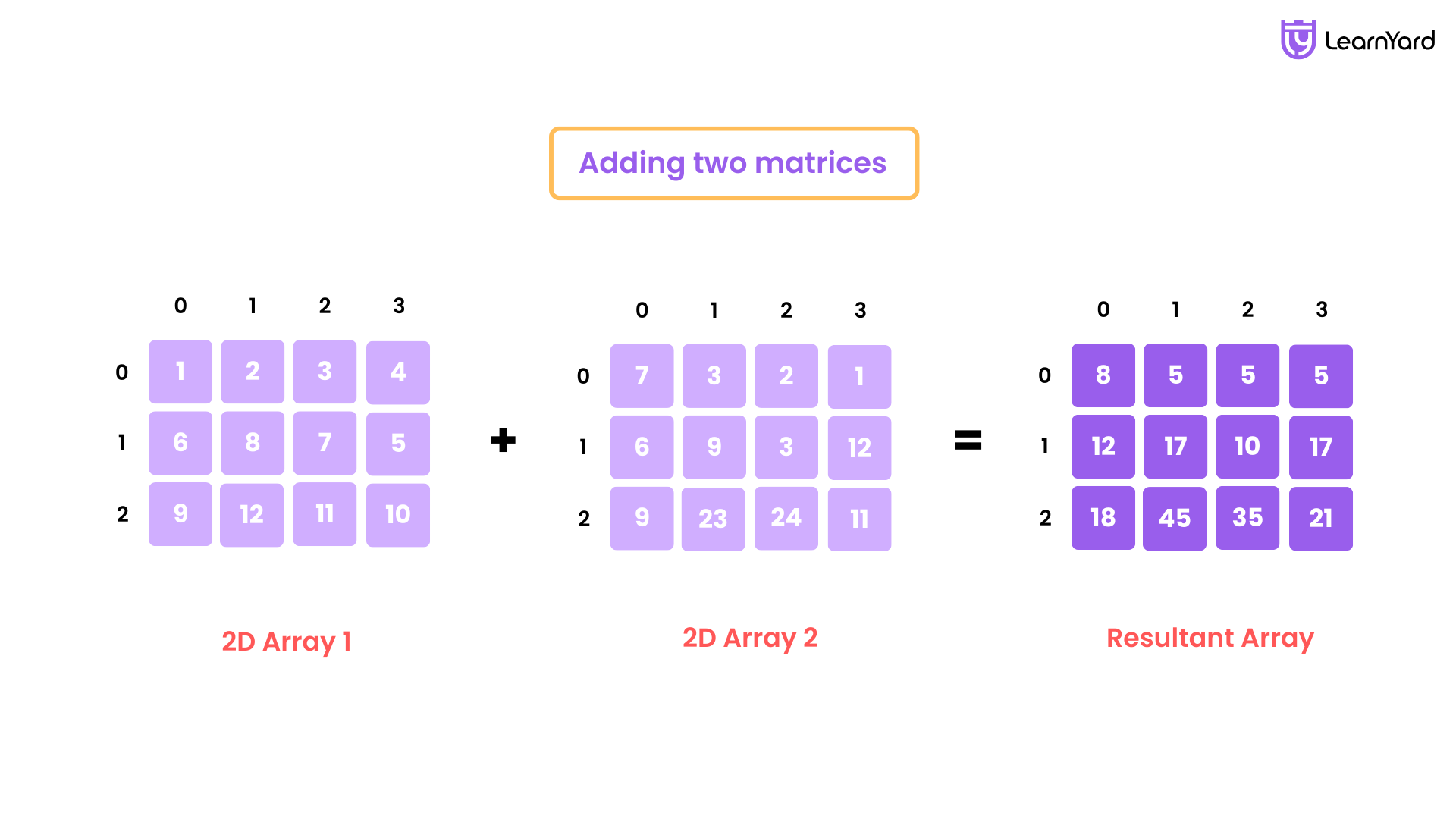
Subtraction: Subtract each element in the second matrix from the corresponding element in the first matrix.

But before, performing the addition between the two 2D-arrays, we have to make sure that the two 2D-Arrays and two empty 2D-array for the purpose of storing the sum and differences have the same dimensions.
Approach
Initialize the Matrices: Begin by defining two matrices, matrix1 and matrix2, containing the values to be added or subtracted. Prepare an empty resultAdd that will store the sum of the operations and the resultDiff that will store the differences of the operations.
Loop through Each Element: For each element at position (i, j) in matrix1 and matrix2, perform the operation:
- Add the element at position (i, j) from matrix1 and matrix2 and store it in resultAdd, or
- Subtract the element at position (i, j) of matrix2 from matrix1 and store it in resultSub.
Store the result of this operation at the corresponding position (i, j) in the resultAdd or resultSub.
Output the Result: After completing the operation for all elements in the matrices, the resultAdd, will contain the addition of the 2D-arrays and the resultSubwill contain the difference of the 2d-arrays.
Print each element of the resultAdd and resultSub row by row to display the outcome.
Dry-Run
Addition: Calculate Each Element in resultAdd
Row 1 (i = 0):
- j = 0: resultAdd[0][0] = matrix1[0][0] + matrix2[0][0] = 1 + 7 = 8
- j = 1: resultAdd[0][1] = matrix1[0][1] + matrix2[0][1] = 2 + 3 = 5
- j = 2: resultAdd[0][2] = matrix1[0][2] + matrix2[0][2] = 3 + 2 = 5
- j = 3: resultAdd[0][3] = matrix1[0][3] + matrix2[0][3] = 4 + 1 = 5
Row 2 (i = 1):
- j = 0: resultAdd[1][0] = matrix1[1][0] + matrix2[1][0] = 6 + 6 = 12
- j = 1: resultAdd[1][1] = matrix1[1][1] + matrix2[1][1] = 8 + 9 = 17
- j = 2: resultAdd[1][2] = matrix1[1][2] + matrix2[1][2] = 7 + 3 = 10
- j = 3: resultAdd[1][3] = matrix1[1][3] + matrix2[1][3] = 5 + 12 = 17
Row 3 (i = 2):
- j = 0: resultAdd[2][0] = matrix1[2][0] + matrix2[2][0] = 9 + 9 = 18
- j = 1: resultAdd[2][1] = matrix1[2][1] + matrix2[2][1] = 12 + 23 = 35
- j = 2: resultAdd[2][2] = matrix1[2][2] + matrix2[2][2] = 11 + 24 = 35
- j = 3: resultAdd[2][3] = matrix1[2][3] + matrix2[2][3] = 10 + 11 = 21
Subtraction: Calculate Each Element in resultSub
Row 1 (i = 0):
- j = 0: resultSub[0][0] = matrix1[0][0] - matrix2[0][0] = 1 - 7 = -6
- j = 1: resultSub[0][1] = matrix1[0][1] - matrix2[0][1] = 2 - 3 = -1
- j = 2: resultSub[0][2] = matrix1[0][2] - matrix2[0][2] = 3 - 2 = 1
- j = 3: resultSub[0][3] = matrix1[0][3] - matrix2[0][3] = 4 - 1 = 3
Row 2 (i = 1):
- j = 0: resultSub[1][0] = matrix1[1][0] - matrix2[1][0] = 6 - 6 = 0
- j = 1: resultSub[1][1] = matrix1[1][1] - matrix2[1][1] = 8 - 9 = -1
- j = 2: resultSub[1][2] = matrix1[1][2] - matrix2[1][2] = 7 - 3 = 4
- j = 3: resultSub[1][3] = matrix1[1][3] - matrix2[1][3] = 5 - 12 = -7
Row 3 (i = 2):
- j = 0: resultSub[2][0] = matrix1[2][0] - matrix2[2][0] = 9 - 9 = 0
- j = 1: resultSub[2][1] = matrix1[2][1] - matrix2[2][1] = 12 - 23 = -11
- j = 2: resultSub[2][2] = matrix1[2][2] - matrix2[2][2] = 11 - 24 = -13
- j = 3: resultSub[2][3] = matrix1[2][3] - matrix2[2][3] = 10 - 11 = -1
Addition Result (resultAdd):
{{8, 5, 5, 5},
{12, 17, 10, 17},
{18, 35, 35, 21}}
Subtraction Result (resultSub):
{{-6, -1, 1, 3},
{0, -1, 4, -7},
{0, -11, -13, -1}}
Code in all Languages
1. C++ Try on Compiler
import java.util.Scanner;
public class MatrixOperations {
// Function to add two matrices
public static void addMatrices(int[][] matrix1, int[][] matrix2, int[][] result) {
int rows = matrix1.length;
int cols = matrix1[0].length;
// Loop through each element of the matrices
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
// Add corresponding elements of matrix1 and matrix2
result[i][j] = matrix1[i][j] + matrix2[i][j];
}
}
}
// Function to subtract two matrices
public static void subtractMatrices(int[][] matrix1, int[][] matrix2, int[][] result) {
int rows = matrix1.length;
int cols = matrix1[0].length;
// Loop through each element of the matrices
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
// Subtract corresponding elements of matrix2 from matrix1
result[i][j] = matrix1[i][j] - matrix2[i][j];
}
}
}
public static void main(String[] args) {
// Hardcoded input matrices
int[][] matrix1 = {{1, 2, 3, 4}, {6, 8, 7, 5}, {9, 12, 11, 10}};
int[][] matrix2 = {{7, 3, 2, 1}, {6, 9, 3, 12}, {9, 23, 24, 11}};
int[][] resultAdd = new int[3][4];
int[][] resultSub = new int[3][4];
// Call the function to add the matrices
addMatrices(matrix1, matrix2, resultAdd);
subtractMatrices(matrix1, matrix2, resultSub);
// Display result of addition
System.out.println("Result of Matrix Addition:");
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
System.out.print(resultAdd[i][j] + " ");
}
System.out.println();
}
// Display result of subtraction
System.out.println("\nResult of Matrix Subtraction:");
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
System.out.print(resultSub[i][j] + " ");
}
System.out.println();
}
// User-defined input
Scanner sc = new Scanner(System.in);
System.out.print("\nEnter dimensions of the matrices (rows cols): ");
int rows = sc.nextInt();
int cols = sc.nextInt();
int[][] userMatrix1 = new int[rows][cols];
int[][] userMatrix2 = new int[rows][cols];
int[][] userResultAdd = new int[rows][cols];
int[][] userResultSub = new int[rows][cols];
System.out.println("Enter elements of matrix1:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
userMatrix1[i][j] = sc.nextInt();
}
}
System.out.println("Enter elements of matrix2:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
userMatrix2[i][j] = sc.nextInt();
}
}
// Add and subtract user matrices
addMatrices(userMatrix1, userMatrix2, userResultAdd);
subtractMatrices(userMatrix1, userMatrix2, userResultSub);
// Display user-defined matrix addition result
System.out.println("User-defined Matrix Addition Result:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
System.out.print(userResultAdd[i][j] + " ");
}
System.out.println();
}
// Display user-defined matrix subtraction result
System.out.println("User-defined Matrix Subtraction Result:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
System.out.print(userResultSub[i][j] + " ");
}
System.out.println();
}
sc.close();
}
}
2. Java Try on Compiler
#include <iostream>
using namespace std;
// Function to add two matrices
void addMatrices(int matrix1[3][4], int matrix2[3][4], int result[3][4]) {
// Loop through each element of the matrices
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
// Add corresponding elements of matrix1 and matrix2
result[i][j] = matrix1[i][j] + matrix2[i][j];
}
}
}
// Function to subtract two matrices
void subtractMatrices(int matrix1[3][4], int matrix2[3][4], int result[3][4]) {
// Loop through each element of the matrices
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
// Subtract corresponding elements of matrix2 from matrix1
result[i][j] = matrix1[i][j] - matrix2[i][j];
}
}
}
int main() {
// Hardcoded input matrices
int matrix1[3][4] = {{1, 2, 3, 4}, {6, 8, 7, 5}, {9, 12, 11, 10}};
int matrix2[3][4] = {{7, 3, 2, 1}, {6, 9, 3, 12}, {9, 23, 24, 11}};
int resultAdd[3][4], resultSub[3][4];
// Call the function to add the matrices
addMatrices(matrix1, matrix2, resultAdd);
// Call the function to subtract the matrices
subtractMatrices(matrix1, matrix2, resultSub);
// Display result of addition
cout << "Result of Matrix Addition:\n";
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
cout << resultAdd[i][j] << " ";
}
cout << endl;
}
// Display result of subtraction
cout << "\nResult of Matrix Subtraction:\n";
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
cout << resultSub[i][j] << " ";
}
cout << endl;
}
// User-defined input
int rows, cols;
cout << "\nEnter dimensions of the matrices: ";
cin >> rows >> cols;
int userMatrix1[rows][cols], userMatrix2[rows][cols], userResultAdd[rows][cols], userResultSub[rows][cols];
cout << "Enter elements of matrix1:\n";
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
cin >> userMatrix1[i][j];
}
}
cout << "Enter elements of matrix2:\n";
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
cin >> userMatrix2[i][j];
}
}
// Add and subtract user matrices
addMatrices(userMatrix1, userMatrix2, userResultAdd);
subtractMatrices(userMatrix1, userMatrix2, userResultSub);
// Display user-defined matrix addition result
cout << "User-defined Matrix Addition Result:\n";
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
cout << userResultAdd[i][j] << " ";
}
cout << endl;
}
// Display user-defined matrix subtraction result
cout << "User-defined Matrix Subtraction Result:\n";
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
cout << userResultSub[i][j] << " ";
}
cout << endl;
}
return 0;
}
3. Python Try on Compiler
# Function to add two matrices
def add_matrices(matrix1, matrix2, rows, cols):
result = [[0 for _ in range(cols)] for _ in range(rows)]
# Loop through each element of the matrices
for i in range(rows):
for j in range(cols):
result[i][j] = matrix1[i][j] + matrix2[i][j]
return result
# Function to subtract two matrices
def subtract_matrices(matrix1, matrix2, rows, cols):
result = [[0 for _ in range(cols)] for _ in range(rows)]
# Loop through each element of the matrices
for i in range(rows):
for j in range(cols):
result[i][j] = matrix1[i][j] - matrix2[i][j]
return result
# Hardcoded input matrices
matrix1 = [[1, 2, 3, 4], [6, 8, 7, 5], [9, 12, 11, 10]]
matrix2 = [[7, 3, 2, 1], [6, 9, 3, 12], [9, 23, 24, 11]]
# Perform operations
result_add = add_matrices(matrix1, matrix2, 3, 4)
result_sub = subtract_matrices(matrix1, matrix2, 3, 4)
# Display results
print("Result of Matrix Addition:")
for row in result_add:
print(row)
print("\nResult of Matrix Subtraction:")
for row in result_sub:
print(row)
# User-defined input
rows, cols = map(int, input("\nEnter dimensions of the matrices (rows cols): ").split())
user_matrix1 = [list(map(int, input(f"Enter row {i+1} of matrix1: ").split())) for i in range(rows)]
user_matrix2 = [list(map(int, input(f"Enter row {i+1} of matrix2: ").split())) for i in range(rows)]
# Add and subtract user matrices
user_result_add = add_matrices(user_matrix1, user_matrix2, rows, cols)
user_result_sub = subtract_matrices(user_matrix1, user_matrix2, rows, cols)
# Display user-defined matrix results
print("User-defined Matrix Addition Result:")
for row in user_result_add:
print(row)
print("User-defined Matrix Subtraction Result:")
for row in user_result_sub:
print(row)
4. JavaScript Try on Compiler
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
// Function to add two matrices
function addMatrices(matrix1, matrix2, rows, cols) {
let result = Array.from({ length: rows }, () => Array(cols).fill(0));
for (let i = 0; i < rows; i++) {
for (let j = 0; j < cols; j++) {
result[i][j] = matrix1[i][j] + matrix2[i][j];
}
}
return result;
}
// Function to subtract two matrices
function subtractMatrices(matrix1, matrix2, rows, cols) {
let result = Array.from({ length: rows }, () => Array(cols).fill(0));
for (let i = 0; i < rows; i++) {
for (let j = 0; j < cols; j++) {
result[i][j] = matrix1[i][j] - matrix2[i][j];
}
}
return result;
}
// Hardcoded input matrices
console.log("Using Hardcoded Input Matrices:");
let matrix1 = [
[1, 2, 3, 4],
[6, 8, 7, 5],
[9, 12, 11, 10]
];
let matrix2 = [
[7, 3, 2, 1],
[6, 9, 3, 12],
[9, 23, 24, 11]
];
// Perform operations on hardcoded matrices
let resultAdd = addMatrices(matrix1, matrix2, 3, 4);
let resultSub = subtractMatrices(matrix1, matrix2, 3, 4);
console.log("Result of Matrix Addition:");
console.table(resultAdd);
console.log("Result of Matrix Subtraction:");
console.table(resultSub);
// User-defined input matrices
console.log("\nUsing User-defined Input:");
rl.question("Enter number of rows: ", (rowsInput) => {
rl.question("Enter number of columns: ", (colsInput) => {
const rows = parseInt(rowsInput);
const cols = parseInt(colsInput);
const userMatrix1 = [];
const userMatrix2 = [];
let rowCounter = 0;
console.log("Enter elements for Matrix 1 row by row:");
// Recursive function to input Matrix 1
function getMatrix1Rows() {
if (rowCounter < rows) {
rl.question(`Row ${rowCounter + 1}: `, (rowInput) => {
userMatrix1.push(rowInput.split(" ").map(Number));
rowCounter++;
getMatrix1Rows();
});
} else {
rowCounter = 0; // Reset row counter for Matrix 2
console.log("Enter elements for Matrix 2 row by row:");
getMatrix2Rows();
}
}
// Recursive function to input Matrix 2
function getMatrix2Rows() {
if (rowCounter < rows) {
rl.question(`Row ${rowCounter + 1}: `, (rowInput) => {
userMatrix2.push(rowInput.split(" ").map(Number));
rowCounter++;
getMatrix2Rows();
});
} else {
// Perform addition and subtraction
const userResultAdd = addMatrices(userMatrix1, userMatrix2, rows, cols);
const userResultSub = subtractMatrices(userMatrix1, userMatrix2, rows, cols);
console.log("User-defined Matrix Addition Result:");
console.table(userResultAdd);
console.log("User-defined Matrix Subtraction Result:");
console.table(userResultSub);
rl.close(); // Close the readline interface
}
}
getMatrix1Rows(); // Start input for Matrix 1
});
});
Time Complexity: O(n x m)
- To add two matrices, we need to iterate over every element in the matrices.
- If the matrices have dimensions n×m times, we perform a constant-time addition operation for each element.
- This results in a time complexity of O(n×m)because we have to visit each element once.
Space Complexity : O(n x m)
Auxiliary Space Complexity: The algorithm does not use any additional data structures or recursive calls beyond the storage for the result matrix.
Thus, the auxiliary space complexity is O(1) if we exclude the result matrix, as the only memory used is for simple variables.
Total Space Complexity: Including the result matrix, we need O(n×m) space to store the sum of the two matrices.
Additionally, if the input matrices are passed to the function and not created within it, we would need space for both input matrices, totalling O(n×m)+O(n×m)=O(n×m) for each matrix.