Skip to main content

Math Basics

Factorial of a Number

The factorial of a non-negative integer n is a mathematical function denoted by n! It represents the product of all positive integers from 1 up to n.

Examples of Factorial

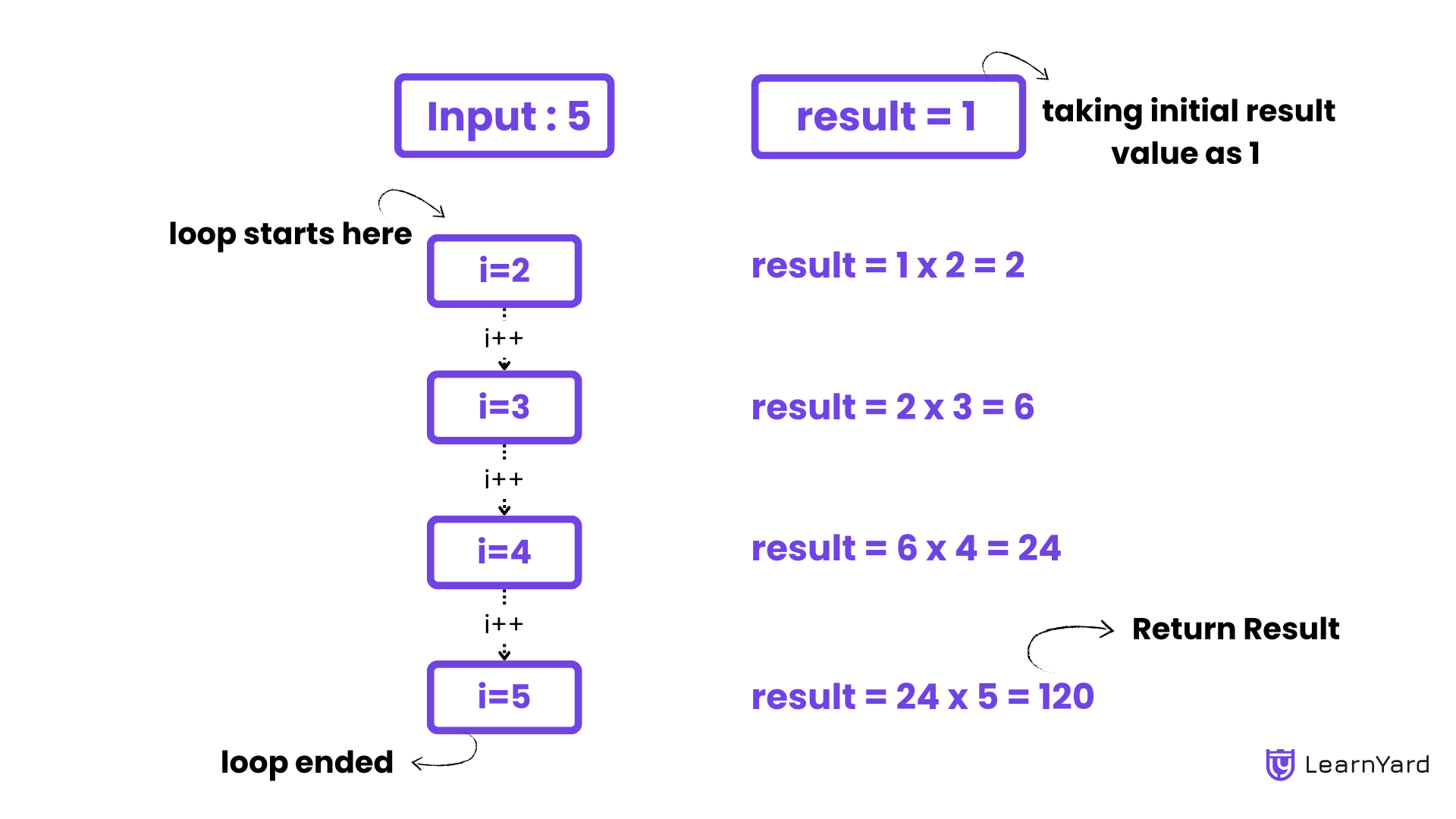
Input: 5
Output: 120
Explanation: 5! is equal to 5*4*3*2*1 = 120.

Input: 4
Output: 24
Explanation: 4! is equal to 4*3*2*1 = 24.

The basic definition of factorial is:  n! = n * (n-1) * (n-2) * (n-3) * ….. * 1.

By definition 0! is equal to 1.

To compute the factorial of a number n, start by initializing a variable result to 1. Then, use a loop that iterates from 1 to n, multiplying the result by each loop counter in each iteration. After completing the loop, the result will contain the factorial of n i.e. n! 

Factorial of a Number

Factorial Program Using a loop

Code Implementation
C++ Code Try on Compiler! 
// Function to calculate factorial using an iterative approach
long long factorial(int n) {
    // Initialize result as 1 (since factorial of 0 is 1)
    long long result = 1; 
    
    // Loop from 1 to n and multiply each number with result
    for (int i = 2; i <= n; i++) {
        result *= i;
    }
    // Return the calculated factorial
    return result; 
}

Java Code Try on Compiler! 
public class Factorial {
    // Function to calculate factorial using an iterative approach
    public static long factorial(int n) {
        long result = 1; // Initialize result as 1
        for (int i = 2; i <= n; i++) {
            result *= i; // Multiply each number with result
        }
        return result; // Return the calculated factorial
    }
}

Python Code Try on Compiler! 
# Function to calculate factorial using an iterative approach
def factorial(n):
    result = 1  # Initialize result as 1
    for i in range(2, n + 1):  # Loop from 2 to n
        result *= i  # Multiply each number with result
    return result  # Return the calculated factorial

Javascript Code Try on Compiler! 
function factorial(n) {
    let result = 1; // Initialize result as 1
    for (let i = 2; i <= n; i++) { // Loop from 2 to n
        result *= i; // Multiply each number with result
    }
    return result; // Return the calculated factorial
}

Time Complexity : O(n)

The time complexity of computing the factorial of n is O(n). This is because the algorithm involves a single loop that iterates from 1 to n. A constant-time operation (multiplication and assignment) is performed in each iteration. Thus, the total time complexity is proportional to the number of iterations, n.

Space Complexity : O(n)

The space complexity of this algorithm is O(1). The algorithm uses a fixed amount of extra space regardless of the input size. It only requires a few variables (like the result and the loop counter), and the amount of memory needed does not grow with n.

Here are some more problems related to this approach -

  1. Reverse a Number
  2. Check Palindrome,
  3. Number System
  4. Divisibility Rules
  5. Divisors of a number
  6. Modulo Arithmetic
  7. Find the number of trailing zeroes in a given factorial of n
  8. Armstrong Number