2D-Arrays I
Having covered the theoretical basics of 2D-Arrays in our previous discussion , let's now apply our basics in solving and understanding 2D-concepts more !!
Q1. How to Print 2D array/matrix row-wise ?

Example
Input : mat[][] = {{1, 2, 3,4}, {5, 6, 7,8}, {9,10,11,12}}
Output : Row-wise: 1 2 3 4 5 6 7 8 9 10 11 12
Approach
Printing a 2D array row-wise asks us to print all the data in each row of the 2D array.
From the above image, is the question asking us to simply print all the elements present in each array of the 2D-Array?
Yes, we can just traverse each 1D array iteratively and print all the elements present in that particular 1D array and then move to the next one.
How many iterations were required to print the whole 2D matrix ?
3 for the three 1D arrays + 4 for the values present in each 1D array.
How to code it ?
Step1 : We will require an outer loop to traverse each array present in the 2D array.The outer loop will iterate from i=0 to i=mat.length.
Step 2: We will require a inner loop to print the elements present in the 2D array. The inner loop will run from j=0 to j=mat[0].length.
Step 3: we will add the print statements inside the inner loop.
Dry-Run
First for Loop (Outer loop): i = 0 (for the first row)
Inner for Loop:
j = 0: Prints mat[0][0] → 1
j = 1: Prints mat[0][1] → 2
j = 2: Prints mat[0][2] → 3
j = 3: Prints mat[0][3] → 4
Output so far: Row-wise: 1 2 3 4
Outer loop (Second Row): i = 1
Inner loop:
j = 0: Prints mat[1][0] → 5
j = 1: Prints mat[1][1] → 6
j = 2: Prints mat[1][2] → 7
j = 3: Prints mat[1][3] → 8
Output so far: Row-wise: 1 2 3 4 5 6 7 8
Outer loop (Third Row): i = 2
Inner loop:
j = 0: Prints mat[2][0] → 9
j = 1: Prints mat[2][1] → 10
j = 2: Prints mat[2][2] → 11
j = 3: Prints mat[2][3] → 12
Final Output for Hardcoded Input: Row-wise: 1 2 3 4 5 6 7 8 9 10 11 12
Code in all Languages
1. C++ Try on Compiler
#include <iostream>
using namespace std;
int main() {
// Hardcoded input
int mat[3][4] = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};
// Output hardcoded matrix row-wise
cout << "Row-wise: ";
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 4; j++) {
cout << mat[i][j] << " ";
}
}
cout << endl;
// User-defined input
int rows, cols;
cout << "Enter number of rows and columns: ";
cin >> rows >> cols;
int userMat[rows][cols];
// Taking user input for each element
cout << "Enter elements of the matrix:" << endl;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
cin >> userMat[i][j];
}
}
// Output user-defined matrix row-wise
cout << "Row-wise: ";
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
cout << userMat[i][j] << " ";
}
}
cout << endl;
return 0;
}2. Java Try on Compiler
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// Hardcoded input
int[][] mat = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};
// Output hardcoded matrix row-wise
System.out.print("Row-wise: ");
for (int i = 0; i < mat.length; i++) {
for (int j = 0; j < mat[i].length; j++) {
System.out.print(mat[i][j] + " ");
}
}
System.out.println();
// User-defined input
Scanner scanner = new Scanner(System.in);
System.out.print("Enter number of rows and columns: ");
int rows = scanner.nextInt();
int cols = scanner.nextInt();
int[][] userMat = new int[rows][cols];
// Taking user input for each element
System.out.println("Enter elements of the matrix:");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
userMat[i][j] = scanner.nextInt();
}
}
// Output user-defined matrix row-wise
System.out.print("Row-wise: ");
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
System.out.print(userMat[i][j] + " ");
}
}
System.out.println();
scanner.close();
}
}
3. Python Try on Compiler
# Hardcoded input
mat = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
]
# Output hardcoded matrix row-wise
print("Row-wise:", end=" ")
for row in mat:
for value in row:
print(value, end=" ")
print()
# User-defined input
rows = int(input("Enter number of rows: "))
cols = int(input("Enter number of columns: "))
# Initialize user-defined matrix
user_mat = []
print("Enter elements of the matrix:")
for i in range(rows):
row = list(map(int, input().split()))
user_mat.append(row)
# Output user-defined matrix row-wise
print("Row-wise:", end=" ")
for row in user_mat:
for value in row:
print(value, end=" ")
print()
4. JavaScript Try on Compiler
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
// Hardcoded input
let mat = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
];
// Output hardcoded matrix row-wise
let rowWiseOutput = "Row-wise: ";
for (let i = 0; i < mat.length; i++) {
for (let j = 0; j < mat[i].length; j++) {
rowWiseOutput += mat[i][j] + " ";
}
}
console.log(rowWiseOutput.trim());
// User-defined input
rl.question('Enter number of rows: ', (rows) => {
rl.question('Enter number of columns: ', (cols) => {
rows = parseInt(rows);
cols = parseInt(cols);
// Initialize user-defined matrix
let userMat = [];
let inputCounter = 0;
console.log("Enter elements of the matrix (space separated):");
function getRow(i) {
rl.question(`Enter row ${i + 1} values: `, (rowInput) => {
let row = rowInput.split(" ").map(Number);
userMat.push(row);
inputCounter++;
if (inputCounter < rows) {
getRow(inputCounter); // Recursively get each row
} else {
// Output user-defined matrix row-wise
rowWiseOutput = "Row-wise: ";
for (let i = 0; i < userMat.length; i++) {
for (let j = 0; j < userMat[i].length; j++) {
rowWiseOutput += userMat[i][j] + " ";
}
}
console.log(rowWiseOutput.trim());
rl.close(); // Close the readline interface after all input is received
}
});
}
getRow(inputCounter); // Start getting the first row
});
});
Time Complexity: O(n x m)
The core operation here is printing all elements of the matrix in a row-wise manner. For a matrix of size n x m, where m is the number of rows and m is the number of columns:
Traversal (Printing each element row-wise):
Time complexity = O(n×m)
Each element of the matrix is accessed and printed once .
Input (User-defined matrix creation):
For user input, if we’re reading each element individually, the time complexity is also
O(n×m) since we need to read each element.
Overall time complexity: O(n×m)
Space Complexity: O(1)
Auxiliary Space Complexity
Auxiliary space complexity refers to any additional space used by the algorithm that is not part of the input.
Hardcoded Input:
The auxiliary space here is minimal since the matrix is already given in the code, so no additional data structures or significant memory is needed.
Auxiliary space complexity = O(1)
Overall auxiliary space complexity: O(1)
Total Space Complexity
The total space complexity includes both the input matrix and any additional memory required.
Hardcoded Matrix:
The matrix size is O(n×m).
User-defined Matrix:
The dynamically allocated matrix also requires O(n×m) space.
Overall total space complexity: O(n×m)
Now that we've seen how to traverse a 2D-Array in a row-wise manner, there are many situations where we need to traverse and perform operations on a 2D-array in column-wise manner as well. Let's explore how this is done with the below problem.
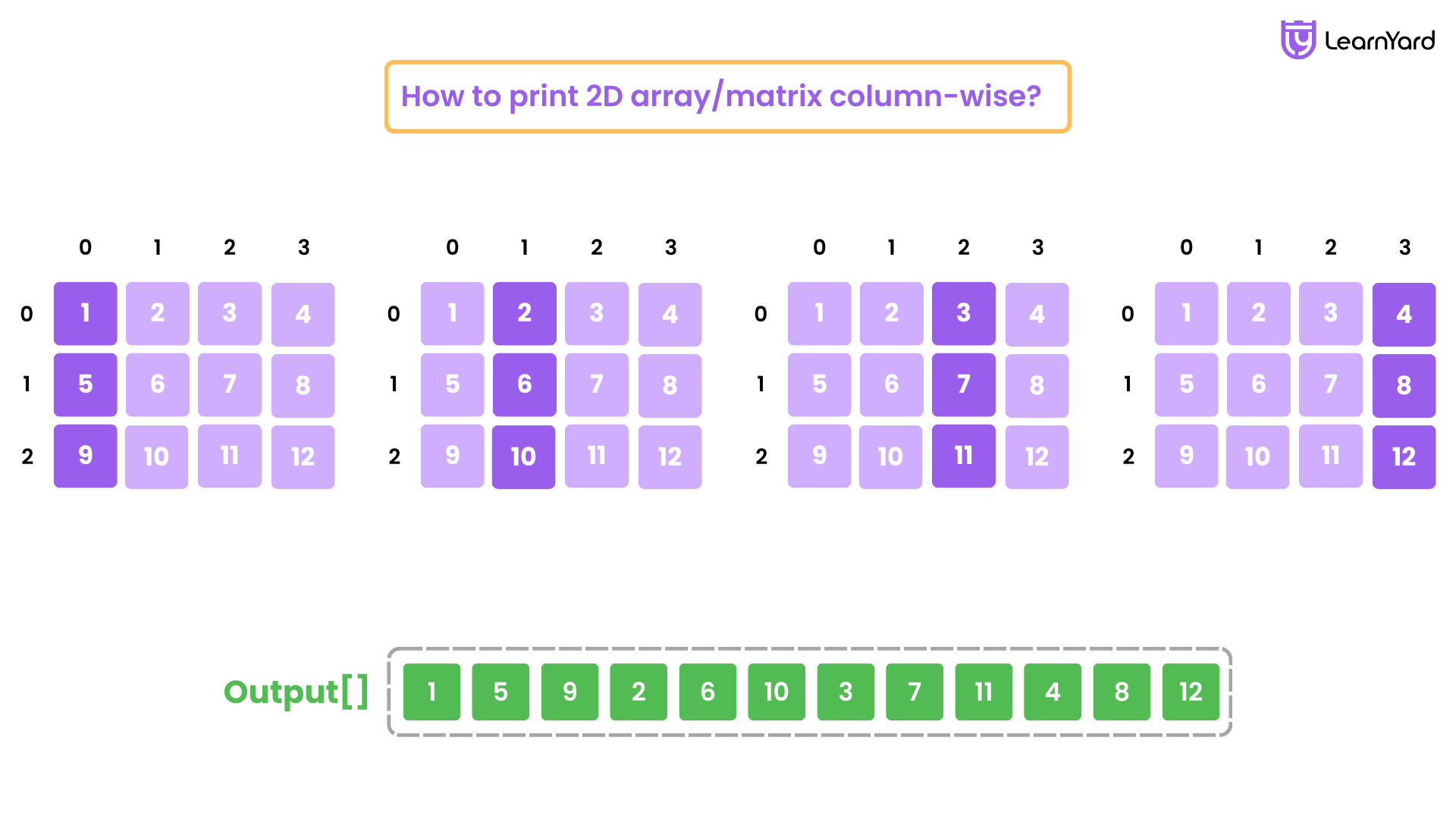
Q2. How to Print 2D array/matrix column-wise ?
Examples
Input : mat[][] = {{1, 2, 3,4}, {5, 6, 7,8}, {9,10,11,12}}
Output : Column-wise: 1 5 9 2 6 10 3 7 11 4 8 12
Approach
Printing a 2D array column-wise asks us to print all the data in each column of the 2D array. To print the matrix in this format, we're printing each element column by column, but within each column, we’re moving down each row. This approach means that we start at the top of each column and print each element going down the column. We move to the next column and repeat until we reach the last column.
Code it up ?
Step 1: For each column we will iterate from j=0 to mat[0].length -1. This means we are first choosing a column to be traversed from top to bottom.
Step2: Next, we will run an inner loop starting from i=0 to i=mat.length.
Step 3: Inside the inner loop we will add the print statements to print mat[i][j].
Dry-Run
Outer loop (First Column): j = 0
Inner loop:
i = 0: Prints mat[0][0] → 1
i = 1: Prints mat[1][0] → 5
i = 2: Prints mat[2][0] → 9
Output so far: Column-wise: 1 5 9
Outer loop (Second Column): j = 1
Inner loop:
i = 0: Prints mat[0][1] → 2
i = 1: Prints mat[1][1] → 6
i = 2: Prints mat[2][1] → 10
Output so far: Column-wise: 1 5 9 2 6 10
Outer loop (Third Column): j = 2
Inner loop:
i = 0: Prints mat[0][2] → 3
i = 1: Prints mat[1][2] → 7
i = 2: Prints mat[2][2] → 11
Output so far: Column-wise: 1 5 9 2 6 10 3 7 11
Outer loop (Fourth Column): j = 3
Inner loop:
i = 0: Prints mat[0][3] → 4
i = 1: Prints mat[1][3] → 8
i = 2: Prints mat[2][3] → 12
Final Output: Column-wise: 1 5 9 2 6 10 3 7 11 4 8 12
Code in all Languages
1. C++ Try on Compiler
#include <iostream>
using namespace std;
int main() {
// Define a hardcoded matrix
int mat[3][4] = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};
// Get user input for custom matrix size
int rows, cols;
cout << "Enter number of rows: ";
cin >> rows;
cout << "Enter number of columns: ";
cin >> cols;
// Initialize matrix for user input
int userMat[rows][cols];
cout << "Enter the matrix elements row by row:" << endl;
// Fill the matrix with user input
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
cin >> userMat[i][j];
}
}
// Choose either hardcoded or user-defined matrix
int (*matrix)[4] = (rows == 0) ? mat : userMat;
// Print the matrix column-wise
cout << "Column-wise: ";
for (int j = 0; j < cols; j++) { // Loop over each column
for (int i = 0; i < rows; i++) { // Loop down each row in the current column
cout << matrix[i][j] << " ";
}
}
cout << endl;
return 0;
}
2. Java Try on Compiler
import java.util.Scanner;
public class ColumnWisePrint {
public static void main(String[] args) {
// Define a hardcoded matrix
int[][] mat = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};
// Get user input for custom matrix size
Scanner scanner = new Scanner(System.in);
System.out.print("Enter number of rows: ");
int rows = scanner.nextInt();
System.out.print("Enter number of columns: ");
int cols = scanner.nextInt();
// Initialize a matrix for user input
int[][] userMat = new int[rows][cols];
System.out.println("Enter the matrix elements row by row:");
// Fill the matrix with user input
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
userMat[i][j] = scanner.nextInt();
}
}
// Choose either hardcoded or user-defined matrix
int[][] matrix = (rows == 0) ? mat : userMat;
// Print the matrix column-wise
System.out.print("Column-wise: ");
for (int j = 0; j < matrix[0].length; j++) { // Loop over each column
for (int i = 0; i < matrix.length; i++) { // Loop down each row in the current column
System.out.print(matrix[i][j] + " ");
}
}
System.out.println();
}
}
3. Python Try on Compiler
# Define the matrix using hardcoded values
mat = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
]
# Ask user for custom input (optional)
rows = int(input("Enter number of rows: "))
cols = int(input("Enter number of columns: "))
# Create an empty matrix to store user input if they prefer
user_mat = []
print("Enter the elements row by row:")
# Fill the matrix with user input
for i in range(rows):
row = list(map(int, input().split()))
user_mat.append(row)
# Choose either hardcoded or user-defined matrix
matrix = mat if rows == 0 else user_mat
# Number of rows and columns in the chosen matrix
rows = len(matrix)
cols = len(matrix[0])
# Print column-wise
print("Column-wise:", end=" ")
for j in range(cols): # Loop over each column
for i in range(rows): # Loop down each row in the current column
print(matrix[i][j], end=" ")
print()
4. JavaScript Try on Compiler
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
// Define a hardcoded matrix
const mat = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
];
// Function to take user input as a 2D array (optional)
function getUserInputMatrix(rows, cols, callback) {
const userMat = [];
let inputCounter = 0;
console.log("Enter the elements row by row:");
function getRow(i) {
rl.question(`Enter row ${i + 1} elements separated by space: `, (rowInput) => {
userMat.push(rowInput.split(" ").map(Number));
inputCounter++;
if (inputCounter < rows) {
getRow(inputCounter); // Recursively get each row
} else {
callback(userMat);
}
});
}
getRow(inputCounter); // Start getting the first row
}
// Get user-defined matrix size
rl.question('Enter number of rows: ', (rowsInput) => {
rl.question('Enter number of columns: ', (colsInput) => {
const rows = Number(rowsInput);
const cols = Number(colsInput);
// Initialize matrix based on user input or use the hardcoded one
const matrix = rows === 0 ? mat : null;
if (matrix) {
printColumnWise(matrix, cols, rows);
rl.close();
} else {
getUserInputMatrix(rows, cols, (userMat) => {
printColumnWise(userMat, cols, rows);
rl.close();
});
}
});
});
// Function to print column-wise
function printColumnWise(matrix, cols, rows) {
let result = "Column-wise: ";
for (let j = 0; j < cols; j++) { // Loop over each column
for (let i = 0; i < rows; i++) { // Loop down each row in the current column
result += matrix[i][j] + " ";
}
}
console.log(result.trim());
}
Time Complexity : O(n x m)
The core operation here is printing all elements of the matrix in a column-wise manner. For a matrix of size n x m, where n is the number of rows and m is the number of columns:
Traversal (Printing each element row-wise):
Time complexity = O(n×m) since each element of the matrix is accessed and printed once.
Input (User-defined matrix creation):
For user input, if we’re reading each element individually, the time complexity is also
O(n×m) since we need to read each element.
Overall time complexity: O(n×m)
Space Complexity : O(1)
Auxiliary Space Complexity
Auxiliary space complexity refers to any additional space used by the algorithm that is not part of the input.
No extra variables and data-structures are used so, auxiliary space complexity = O(1)
Total Space Complexity
The total space complexity includes both the input matrix and any additional memory required.
Hardcoded Matrix:
The matrix size is O(N×M).
User-defined Matrix:
The dynamically allocated matrix also requires O(N×M) space.
Overall total space complexity: O(N×M)
Since, we came to know the ways to print the 2D array/matrix , we are clear how we can traverse a 2D-array in different ways.
In certain scenarios we will be asked to manipulate the values present inside the 2D-Array. Let's learn it !!
Q3. Total Sum of Matrix
Example
Input : mat[][] = {{1, 2, 3,4}, {5, 6, 7,8}, {9,10,11,12}}
Output : 78
Explanation: Sum of all elements inside mat[][] is 78.
Intuition
We are given a 2D-Array, we have to find out the sum of all elements in the given 2D-Array.
Since we have learned the ways to traverse the whole matrix, while traversing can we just add those elements in a variable and then return it?
In the previous question we were just printing the elements. What shall we do now when we encounter elements ?
We can just follow either of the row wise traversal or the column-wise traversal.
We will simply maintain a sum variable of int/long data-type based on the constraints and whenever we encounter an element we will add to the sum variable. At the end of the whole 2D-Array , we will get the sum of all elements inside it.
Approach
Initialize Sum Variable: Declare an integer variable sumElements and set it to 0. This will store the sum of all elements in the chosen matrix.
Calculate the Sum of Matrix Elements: Traverse through the chosen matrix row by row:
- Outer Loop: Iterate through each row (i) of the matrix.
- Inner Loop: Iterate through each column (j) of the current row.
- Add the element at the current position (matrix[i][j]) to the variable sumElements.
Output the Sum: Print the value of sumElements, which represents the sum of all elements in the matrix.
Dry-Run
Initial Setup
mat is a 3x4 matrix, so rows = 3 and cols = 4.
We initialize sumElements = 0.
Calculating the Sum
Loop through each row and column to add elements:
First Row (i = 0):
j = 0: sumElements += mat[0][0] → sumElements = 0 + 1 = 1
j = 1: sumElements += mat[0][1] → sumElements = 1 + 2 = 3
j = 2: sumElements += mat[0][2] → sumElements = 3 + 3 = 6
j = 3: sumElements += mat[0][3] → sumElements = 6 + 4 = 10
Sum after First Row: 10
Second Row (i = 1):
j = 0: sumElements += mat[1][0] → sumElements = 10 + 5 = 15
j = 1: sumElements += mat[1][1] → sumElements = 15 + 6 = 21
j = 2: sumElements += mat[1][2] → sumElements = 21 + 7 = 28
j = 3: sumElements += mat[1][3] → sumElements = 28 + 8 = 36
Sum after Second Row: 36
Third Row (i = 2):
j = 0: sumElements += mat[2][0] → sumElements = 36 + 9 = 45
j = 1: sumElements += mat[2][1] → sumElements = 45 + 10 = 55
j = 2: sumElements += mat[2][2] → sumElements = 55 + 11 = 66
j = 3: sumElements += mat[2][3] → sumElements = 66 + 12 = 78
Sum after Third Row: 78
Result
The final sum, sumElements, is 78, which is printed as:
Sum of all elements: 78
Code in all Languages
1. C++ Try on Compiler
#include <iostream>
using namespace std;
int main() {
// Define a hardcoded matrix
int mat[3][4] = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};
// Get user input for custom matrix size
int rows, cols;
cout << "Enter number of rows: ";
cin >> rows;
cout << "Enter number of columns: ";
cin >> cols;
// Initialize a matrix for user input
int userMat[rows][cols];
cout << "Enter the matrix elements row by row:" << endl;
// Loop to fill the matrix with user input
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
cin >> userMat[i][j];
}
}
// Choose the matrix to use (hardcoded or user-defined)
int (*matrix)[4] = (rows == 0) ? mat : userMat;
// Initialize sum variable to store the sum of all elements
int sumElements = 0;
// Traverse the matrix row by row
for (int i = 0; i < rows; i++) { // Loop over each row
for (int j = 0; j < cols; j++) { // Loop over each element in the row
sumElements += matrix[i][j]; // Add each element to the total sum
}
}
// Print the calculated sum
cout << "Sum of all elements: " << sumElements << endl;
return 0;
}
2. Java Try on Compiler
import java.util.Scanner;
public class MatrixSum {
public static void main(String[] args) {
// Define a hardcoded matrix
int[][] mat = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};
// Get user input for custom matrix size
Scanner scanner = new Scanner(System.in);
System.out.print("Enter number of rows: ");
int rows = scanner.nextInt();
System.out.print("Enter number of columns: ");
int cols = scanner.nextInt();
// Initialize a matrix for user input
int[][] userMat = new int[rows][cols];
System.out.println("Enter the matrix elements row by row:");
// Loop to fill the matrix with user input
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
userMat[i][j] = scanner.nextInt();
}
}
// Choose the matrix to use (hardcoded or user-defined)
int[][] matrix = (rows == 0) ? mat : userMat;
// Initialize sum variable to store the sum of all elements
int sumElements = 0;
// Traverse the matrix row by row
for (int i = 0; i < matrix.length; i++) { // Loop over each row
for (int j = 0; j < matrix[i].length; j++) { // Loop over each element in the row
sumElements += matrix[i][j]; // Add each element to the total sum
}
}
// Print the calculated sum
System.out.println("Sum of all elements: " + sumElements);
}
}
3. Python Try on Compiler
# Define the matrix using hardcoded values
mat = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
]
# Prompt user for custom input (optional)
rows = int(input("Enter number of rows: "))
cols = int(input("Enter number of columns: "))
# Initialize an empty matrix for user input
user_mat = []
print("Enter the elements row by row:")
# Loop to fill the matrix with user input
for i in range(rows):
row = list(map(int, input().split()))
user_mat.append(row)
# Choose the matrix to use (hardcoded or user-defined)
matrix = mat if rows == 0 else user_mat
# Initialize sum variable to store the sum of all elements
sum_elements = 0
# Traverse the matrix row by row
for row in matrix: # Loop over each row
for element in row: # Loop over each element in the row
sum_elements += element # Add each element to the total sum
# Print the calculated sum
print("Sum of all elements:", sum_elements)
4. JavaScript Try on Compiler
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
// Define a hardcoded matrix
const mat = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
];
// Function to take user input as a 2D array (optional)
function getUserInputMatrix(rows, cols, callback) {
const userMat = [];
let inputCounter = 0;
console.log("Enter the elements row by row:");
function getRow(i) {
rl.question(`Enter row ${i + 1} elements separated by space: `, (rowInput) => {
userMat.push(rowInput.split(" ").map(Number));
inputCounter++;
if (inputCounter < rows) {
getRow(inputCounter); // Recursively get each row
} else {
callback(userMat);
}
});
}
getRow(inputCounter); // Start getting the first row
}
// Get user-defined matrix size
rl.question('Enter number of rows: ', (rowsInput) => {
rl.question('Enter number of columns: ', (colsInput) => {
const rows = Number(rowsInput);
const cols = Number(colsInput);
// Initialize matrix based on user input or use the hardcoded one
const matrix = rows === 0 ? mat : null;
if (matrix) {
printColumnWise(matrix, cols, rows);
rl.close();
} else {
getUserInputMatrix(rows, cols, (userMat) => {
printColumnWise(userMat, cols, rows);
rl.close();
});
}
});
});
// Function to print column-wise
function printColumnWise(matrix, cols, rows) {
let result = "Column-wise: ";
for (let j = 0; j < cols; j++) { // Loop over each column
for (let i = 0; i < rows; i++) { // Loop down each row in the current column
result += matrix[i][j] + " ";
}
}
console.log(result.trim());
}
Time Complexity: O(n x m)
The core operation here is printing all elements of the matrix in a column-wise manner. For a matrix of size n x m, where n is the number of rows and m is the number of columns:
Traversal (Printing each element row-wise):
Time complexity = O(n×m)
Each element of the matrix is accessed and printed once.
Input (User-defined matrix creation):
For user input, if we’re reading each element individually, the time complexity is also
O(n×m) since we need to read each element.
Overall time complexity: O(n×m)
Space Complexity : O(1)
Auxiliary Space Complexity: Auxiliary space complexity considers any extra space used by the algorithm that does not include the input data.
- Matrix Storage: We do not create additional data structures; we only use variables for loop counters and the sum.
- Loop Variables: The space for loop variables (e.g., iterators) is constant.
Therefore, the auxiliary space complexity is: O(1)
Total Space Complexity: Total space complexity includes both the input matrix and any additional space used by the algorithm.
- Input Matrix: The matrix itself takes up space proportional to the number of elements, which is n×m
- Auxiliary Space: As calculated above, auxiliary space is O(1)
Thus, the total space complexity is: O(n×m)
Since, we have learned how to find sum of all elements in a 2D array,
What if we are asked to find the sum of each row and each column in a 2D array/matrix? We have to make sure that "Row wise traversal" and "column wise traversal" are known to us !!
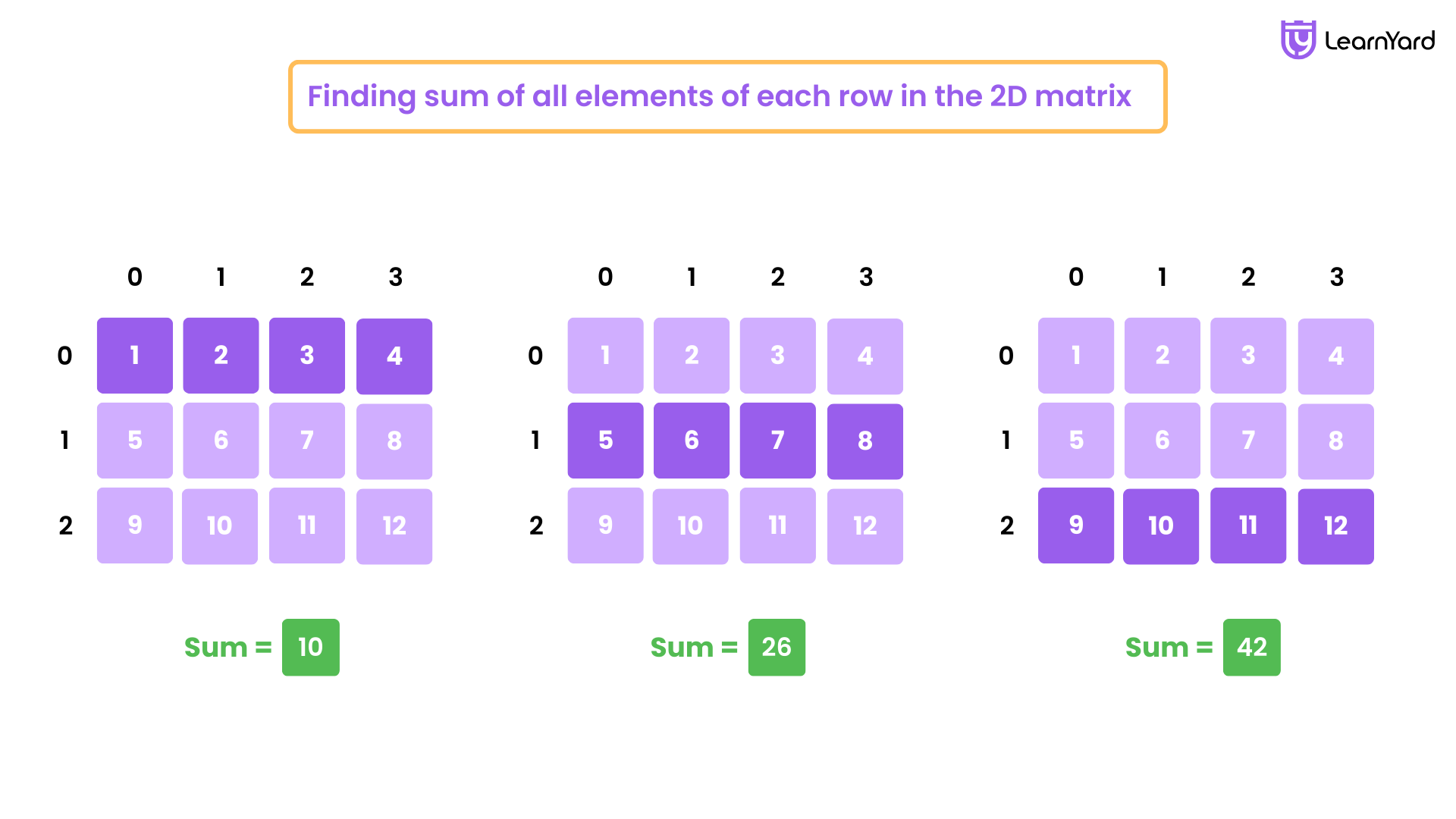
Q4. Finding sum of all elements of each row in the 2D matrix.
Example
Input : mat[][] = {{1, 2, 3,4},
{5, 6, 7,8},
{9,10,11,12}}
Output : Sum of Row 1: 10
Sum of Row 2: 26
Sum of Row 3: 42
Intuition
We are given a 2D-array of size of n x m. We are asked to find the sum of all numbers in each row.
We have learnt a way to traverse the 2D array row-wise.
Aren't we asked to calculate the sum of elements of each row of the 2D array?
Yes, we can blindly follow the row-wise traversal for finding the sum of all elements of each row.
Approach
Loop through each row in the matrix: Use a loop variable i to iterate over rows (from 0 to matrix.size() - 1). We will initialize a variable sum to 0 to store the sum of elements in the current row.
Sum elements of the current row: We can use a nested loop with variable j to iterate over each column in the row (from 0 to matrix[i].size() - 1) and then add the element at position matrix[i][j] to sum.
Print the sum of the current row: Display a message: "Sum of Row X: sum", where X is the 1-based row index (i + 1), and sum is the calculated sum.
Dry-Run
First Iteration (i = 0, First Row: {1, 2, 3, 4})
Initialize sum = 0
Add 1 to sum: sum = 1
Add 2 to sum: sum = 3
Add 3 to sum: sum = 6
Add 4 to sum: sum = 10
Output: Sum of Row 1: 10
Second Iteration (i = 1, Second Row: {5, 6, 7, 8})
Initialize sum = 0
Add 5 to sum: sum = 5
Add 6 to sum: sum = 11
Add 7 to sum: sum = 18
Add 8 to sum: sum = 26
Output: Sum of Row 2: 26
Third Iteration (i = 2, Third Row: {9, 10, 11, 12})
Initialize sum = 0
Add 9 to sum: sum = 9
Add 10 to sum: sum = 19
Add 11 to sum: sum = 30
Add 12 to sum: sum = 42
Output: Sum of Row 3: 42
Using Hardcoded Input:
Sum of Row 1: 10
Sum of Row 2: 26
Sum of Row 3: 42
Code in all Languages
1. C++ Try on Compiler
#include <iostream>
#include <vector>
using namespace std;
// Function to calculate the sum of each row in the matrix
void rowSum(const vector<vector<int>>& matrix) {
// Loop through each row
for (int i = 0; i < matrix.size(); i++) {
int sum = 0; // Initialize sum for the current row
// Sum up elements of the current row
for (int j = 0; j < matrix[i].size(); j++) {
sum += matrix[i][j];
}
// Display the sum of the current row (1-based index)
cout << "Sum of Row " << (i + 1) << ": " << sum << endl;
}
}
int main() {
// Hardcoded matrix
cout << "Using Hardcoded Input:" << endl;
vector<vector<int>> matrixHardcoded = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};
// Call the function with hardcoded matrix
rowSum(matrixHardcoded);
// User-defined input
cout << "\nUsing User-defined Input:" << endl;
int rows, cols;
cout << "Enter the number of rows: ";
cin >> rows;
cout << "Enter the number of columns: ";
cin >> cols;
// Initialize the matrix with user-defined size
vector<vector<int>> matrixUser(rows, vector<int>(cols));
// Take input for each row
for (int i = 0; i < rows; i++) {
cout << "Enter elements for row " << (i + 1) << ": ";
for (int j = 0; j < cols; j++) {
cin >> matrixUser[i][j];
}
}
// Calculate row sums for the user-defined matrix
rowSum(matrixUser);
return 0;
}
2. Java Try on Compiler
import java.util.Scanner;
public class RowSumMatrix {
// Function to calculate the sum of each row in the matrix
static void rowSum(int[][] matrix) {
// Loop through each row
for (int i = 0; i < matrix.length; i++) {
int sum = 0; // Initialize sum for the current row
// Sum up elements of the current row
for (int j = 0; j < matrix[i].length; j++) {
sum += matrix[i][j];
}
// Display the sum of the current row (1-based index)
System.out.println("Sum of Row " + (i + 1) + ": " + sum);
}
}
public static void main(String[] args) {
// Hardcoded matrix
System.out.println("Using Hardcoded Input:");
int[][] matrixHardcoded = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};
// Call the function with hardcoded matrix
rowSum(matrixHardcoded);
// User-defined input
System.out.println("\nUsing User-defined Input:");
Scanner scanner = new Scanner(System.in);
// Take the number of rows and columns
System.out.print("Enter the number of rows: ");
int rows = scanner.nextInt();
System.out.print("Enter the number of columns: ");
int cols = scanner.nextInt();
// Initialize the matrix
int[][] matrixUser = new int[rows][cols];
// Take input for each row
for (int i = 0; i < rows; i++) {
System.out.println("Enter elements for row " + (i + 1) + ":");
for (int j = 0; j < cols; j++) {
matrixUser[i][j] = scanner.nextInt();
}
}
// Calculate row sums for the user-defined matrix
rowSum(matrixUser);
scanner.close();
}
}
3. Python Try on Compiler
# Function to calculate the sum of each row in the matrix
def row_sum(matrix):
# Iterate through each row using a loop and print the sum
for i, row in enumerate(matrix):
# Calculate the sum of the current row
row_sum = sum(row)
# Print the sum of the current row with row number (1-based index)
print(f"Sum of Row {i + 1}: {row_sum}")
# Hardcoded input matrix
print("Using Hardcoded Input:")
matrix_hardcoded = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
]
# Call the function with hardcoded input
row_sum(matrix_hardcoded)
# Accepting user-defined input for the matrix
print("\nUsing User-defined Input:")
# Taking the number of rows from the user
rows = int(input("Enter the number of rows: "))
# Initialize an empty list to store the user-defined matrix
matrix_user = []
# Loop through each row to get user input
for i in range(rows):
# Take input for each row and convert it to a list of integers
row = list(map(int, input(f"Enter row {i + 1} elements separated by spaces: ").split()))
# Append the row to the matrix
matrix_user.append(row)
# Call the function with user-defined input
row_sum(matrix_user)
4. JavaScript Try on Compiler
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
});
// Function to calculate the sum of each row in the matrix
function rowSum(matrix) {
// Loop through each row
for (let i = 0; i < matrix.length; i++) {
let sum = 0; // Initialize sum for the current row
// Sum up elements of the current row
for (let j = 0; j < matrix[i].length; j++) {
sum += matrix[i][j];
}
// Display the sum of the current row (1-based index)
console.log(`Sum of Row ${i + 1}: ${sum}`);
}
}
// Hardcoded matrix
console.log("Using Hardcoded Input:");
const matrixHardcoded = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
];
// Call the function with the hardcoded matrix
rowSum(matrixHardcoded);
// User-defined input using readline
console.log("\nUsing User-defined Input:");
rl.question('Enter the number of rows: ', (rowsInput) => {
rl.question('Enter the number of columns: ', (colsInput) => {
const rows = parseInt(rowsInput);
const cols = parseInt(colsInput);
const matrixUser = [];
let rowCounter = 0;
// Function to collect each row
function getRowInput() {
if (rowCounter < rows) {
rl.question(`Enter elements for row ${rowCounter + 1} separated by spaces: `, (rowInput) => {
matrixUser.push(rowInput.split(" ").map(Number));
rowCounter++;
getRowInput(); // Continue to next row
});
} else {
// After all rows are collected, calculate the row sums
rowSum(matrixUser);
rl.close(); // Close the readline interface
}
}
getRowInput(); // Start collecting rows
});
});
Time Complexity: O(n x m)
The code iterates through each element of the matrix once to compute the sum of each row.
Since there are n rows and m columns, the function iterates through a total of n x m elements.
Therefore, the time complexity is: O(n×m)
Space Complexity: O(1)
Auxiliary Space Complexity
Auxiliary space is the extra space required by the algorithm (excluding input data):
The algorithm requires a few temporary variables, like sum and loop indices (i and j), which have constant space i.e. O(1).
Thus, the auxiliary space complexity is: O(1)
Total Space Complexity
Total space includes the input data, so:
- The matrix itself has N rows and M columns, requiring N space to store.
- Adding this to the auxiliary space complexity, the total space complexity is: O(N×M)
Since, we have learnt how to find the sum of all elements of each row of a 2D-matrix. Let's now dive into another such problem.
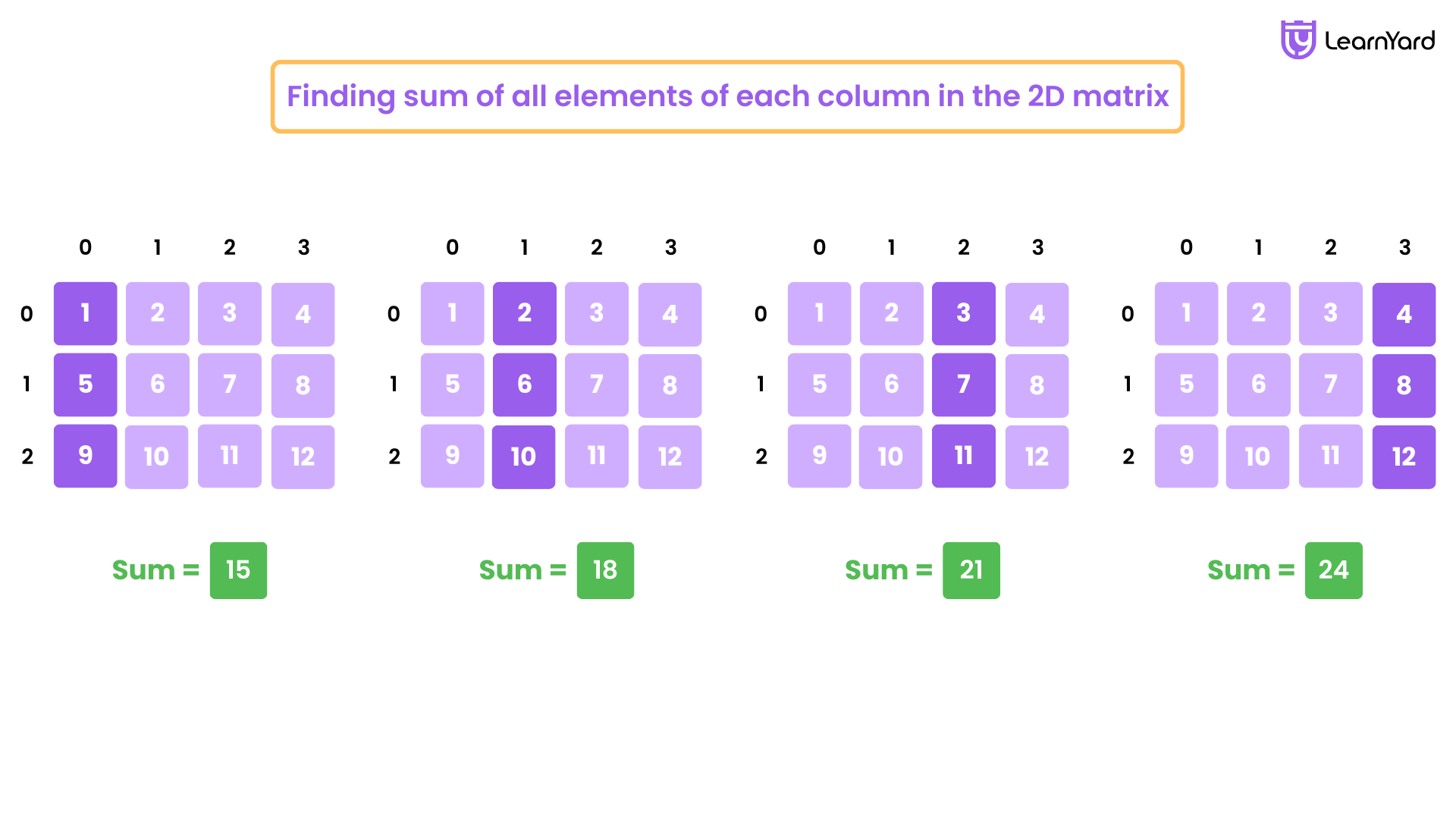
Q5. Finding sum of all elements of each column in the 2D matrix.
Example
Input : mat[][] = {{1, 2, 3,4},
{5, 6, 7,8},
{9,10,11,12}}
Output : Sum of Column 1: 15
Sum of Column 2: 18
Sum of Column 3: 21
Sum of Column 4: 24
Intuition
We are given a 2D-array of size of n x m. We are asked to find the sum of all numbers in each coulmn.
To find the sum of each column in a matrix, we need to look at each column individually and add up all the numbers in that column across all rows.
Since, we learnt the column-wise traversal , can we make use of it and find the sum of each column in that matrix ?
What we will be doing is:
1. Start with the first column, then the second, and so on.
2. For each column, add up the numbers in that column across all rows.
3. Print the sum for each column after going through all rows.
Approach
Loop through each column: Use a loop variable j to iterate through the columns (from 0 to matrix[0].size() - 1).
Initialize the column sum: Declare a variable sum and set it to 0. This will store the sum of the current column.
Sum up elements in the current column: Use a nested loop with a variable i to iterate through each row in the column (from 0 to matrix.size() - 1). Add the element at position matrix[i][j] (row i and column j) to the variable sum.
Print the column sum: Display a message: "Sum of Column X: sum", where X is the 1-based column index (j + 1), and sum is the calculated sum for the column.
Dry-Run
Outer Loop Iterations (Each Column)First Column (j = 0):
Initialize sum = 0 for Column 1.
Inner loop over rows for Column 1:
matrix[0][0] = 1; add 1 to sum → sum = 1
matrix[1][0] = 5; add 5 to sum → sum = 6
matrix[2][0] = 9; add 9 to sum → sum = 15
End of inner loop for Column 1.
Print: "Sum of Column 1: 15"
Second Column (j = 1):
Initialize sum = 0 for Column 2.
Inner loop over rows for Column 2:
matrix[0][1] = 2; add 2 to sum → sum = 2
matrix[1][1] = 6; add 6 to sum → sum = 8
matrix[2][1] = 10; add 10 to sum → sum = 18
End of inner loop for Column 2.
Print: "Sum of Column 2: 18"
Third Column (j = 2):
Initialize sum = 0 for Column 3.
Inner loop over rows for Column 3:
matrix[0][2] = 3; add 3 to sum → sum = 3
matrix[1][2] = 7; add 7 to sum → sum = 10
matrix[2][2] = 11; add 11 to sum → sum = 21
End of inner loop for Column 3.
Print: "Sum of Column 3: 21"
Fourth Column (j = 3):
Initialize sum = 0 for Column 4.
Inner loop over rows for Column 4:
matrix[0][3] = 4; add 4 to sum → sum = 4
matrix[1][3] = 8; add 8 to sum → sum = 12
matrix[2][3] = 12; add 12 to sum → sum = 24
End of inner loop for Column 4.
Print: "Sum of Column 4: 24"
Final Output
After completing all iterations, the program outputs:
Sum of Column 1: 15
Sum of Column 2: 18
Sum of Column 3: 21
Sum of Column 4: 24
Code in all Languages
1. C++ Try on Compiler
#include <iostream>
#include <vector>
using namespace std;
// Function to calculate the sum of each column in the matrix
void columnSum(const vector<vector<int>>& matrix) {
// Loop through each column
for (int j = 0; j < matrix[0].size(); j++) {
int sum = 0; // Initialize sum for the current column
// Sum up elements of the current column
for (int i = 0; i < matrix.size(); i++) {
sum += matrix[i][j];
}
// Display the sum of the current column (1-based index)
cout << "Sum of Column " << (j + 1) << ": " << sum << endl;
}
}
int main() {
// Hardcoded matrix
cout << "Using Hardcoded Input:" << endl;
vector<vector<int>> matrixHardcoded = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};
// Call the function with hardcoded matrix
columnSum(matrixHardcoded);
// User-defined input
cout << "\nUsing User-defined Input:" << endl;
int rows, cols;
cout << "Enter the number of rows: ";
cin >> rows;
cout << "Enter the number of columns: ";
cin >> cols;
// Initialize the matrix
vector<vector<int>> matrixUser(rows, vector<int>(cols));
// Take input for each element in the matrix
for (int i = 0; i < rows; i++) {
cout << "Enter elements for row " << (i + 1) << ": ";
for (int j = 0; j < cols; j++) {
cin >> matrixUser[i][j];
}
}
// Calculate column sums for the user-defined matrix
columnSum(matrixUser);
return 0;
}
2. Java Try on Compiler
import java.util.Scanner;
public class ColumnSumMatrix {
// Function to calculate the sum of each column in the matrix
static void columnSum(int[][] matrix) {
// Loop through each column
for (int j = 0; j < matrix[0].length; j++) {
int sum = 0; // Initialize sum for the current column
// Sum up elements of the current column
for (int i = 0; i < matrix.length; i++) {
sum += matrix[i][j];
}
// Display the sum of the current column (1-based index)
System.out.println("Sum of Column " + (j + 1) + ": " + sum);
}
}
public static void main(String[] args) {
// Hardcoded matrix
System.out.println("Using Hardcoded Input:");
int[][] matrixHardcoded = {
{1, 2, 3, 4},
{5, 6, 7, 8},
{9, 10, 11, 12}
};
// Call the function with hardcoded matrix
columnSum(matrixHardcoded);
// User-defined input
System.out.println("\nUsing User-defined Input:");
Scanner scanner = new Scanner(System.in);
// Take the number of rows and columns
System.out.print("Enter the number of rows: ");
int rows = scanner.nextInt();
System.out.print("Enter the number of columns: ");
int cols = scanner.nextInt();
// Initialize the matrix
int[][] matrixUser = new int[rows][cols];
// Take input for each element in the matrix
for (int i = 0; i < rows; i++) {
System.out.println("Enter elements for row " + (i + 1) + ":");
for (int j = 0; j < cols; j++) {
matrixUser[i][j] = scanner.nextInt();
}
}
// Calculate column sums for the user-defined matrix
columnSum(matrixUser);
scanner.close();
}
}
3. Python Try on Compiler
def column_sum(matrix):
# Loop through each column by index
for j in range(len(matrix[0])):
sum_col = 0 # Initialize sum for the current column
# Sum up elements of the current column
for i in range(len(matrix)):
sum_col += matrix[i][j]
# Display the sum of the current column (1-based index)
print(f"Sum of Column {j + 1}: {sum_col}")
# Hardcoded matrix
print("Using Hardcoded Input:")
matrix_hardcoded = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
]
column_sum(matrix_hardcoded)
# User-defined input
print("\nUsing User-defined Input:")
rows = int(input("Enter the number of rows: "))
cols = int(input("Enter the number of columns: "))
# Initialize the matrix
matrix_user = []
for i in range(rows):
print(f"Enter elements for row {i + 1}:")
row = list(map(int, input().split()))
matrix_user.append(row)
# Calculate column sums for the user-defined matrix
column_sum(matrix_user)
4. JavaScript Try on Compiler
// Function to calculate the sum of each column in the matrix
function columnSum(matrix) {
// Loop through each column by index
for (let j = 0; j < matrix[0].length; j++) {
let sum = 0; // Initialize sum for the current column
// Sum up elements of the current column
for (let i = 0; i < matrix.length; i++) {
sum += matrix[i][j];
}
// Display the sum of the current column (1-based index)
console.log("Sum of Column " + (j + 1) + ": " + sum);
}
}
// Hardcoded matrix
console.log("Using Hardcoded Input:");
const matrixHardcoded = [
[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]
];
columnSum(matrixHardcoded);
// User-defined input requires a prompt or manual setup, as the example is suited for environments without direct input.
Time Complexity: O(n x m)
The time complexity of the depends upon the function that iterates through each element of the matrix once to compute the sum of each row. Since there are n rows and m columns, the function iterates through a total of n x m elements.
Therefore, the time complexity is: O(n×m)
Space Complexity: O(1)
Auxiliary Space Complexity
Auxiliary space is the extra space required by the algorithm (excluding input data):
The rwoSum function requires a few temporary variables, like sum and loop indices (i and j), which have constant space.
Thus, the auxiliary space complexity is: O(1)
Total Space Complexity
Total space includes the input data, so:
- The matrix itself has N rows and M columns, requiring N space to store.
- Adding this to the auxiliary space complexity, the total space complexity is: O(N×M)