Reverse a Given Number
Given an integer num, reverse the digits of the number and return the reversed number.
Examples
Input: 687
Output: 786
Explanation: If we reverse the number 687, we will get 786.
Input: 120
Output: 21
Explanation: If we reverse the number 120, we will get 021 so after removing trailing zeroes we get 21.
Intuition
Before diving deep into the problem, we knew exacting the digits from a number.
Now in this question, we are told to reverse a number.
So, can extracting the digits from the number can help us solve this problem?
so the answer is yes it can! If you closely observe, extracting the number we were getting the last digit at first, then the second last digit, then the third last digit, and so on till the first digit.
Now after extraction of digits, we know we are getting the digits in the reverse order of the initial number, so now we just have to combine those extracted digits to form a new number which is the reverse of the initial number.
So, how will we do this?
Let us understand it with an example where the number is 123.
We can write 123 as 1*(10^2) + 2*(10^1) + 3*(10^0) (So 1 is in the hundred places, 2 is in the tens place and 3 is in one's place)
Now, after extracting the digits, they are in the order 3, 2, 1. So, we just need to combine them to form the reversed number. To do this, we will simply multiply 3 by the most significant power, 2 by the second-most significant power, and 1 by the least significant power.
So it will be like 3*(10^2) + 2*(10^1) + 1*( 10^0) = 321.
Now we can say we can form the reverse number of a number by combining the extracted digits by multiplying each one of them to the power of 10 (higher to lower) and summing them up.
In general, the formula is,
di is the i-th digit of the number N when reading from right to left (starting from the least significant digit).k is the total number of digits in N minus 1.
So, this is one of the methods we can follow, where we multiply the last digit by 10^k, the second-last digit by 10^(k-1), and so on. For this method, we first need to determine the length (k) of the given number and then perform the operations we discussed.
However, this method requires extra space to store the extracted digits. To avoid this additional space, we can declare a reversedNumber variable and can store data in a single pass while extracting the digits.
Approach
This approach reverses the digits of a given number n. It works by repeatedly extracting the last digit of n using the modulus operator (n % 10) and appending it to the reverse number (reversedNumber). After extracting the digit, the number n is reduced by dividing it by 10 (n = n / 10). This process continues until n becomes 0. Finally, the reversed number (reversedNumber) is returned.
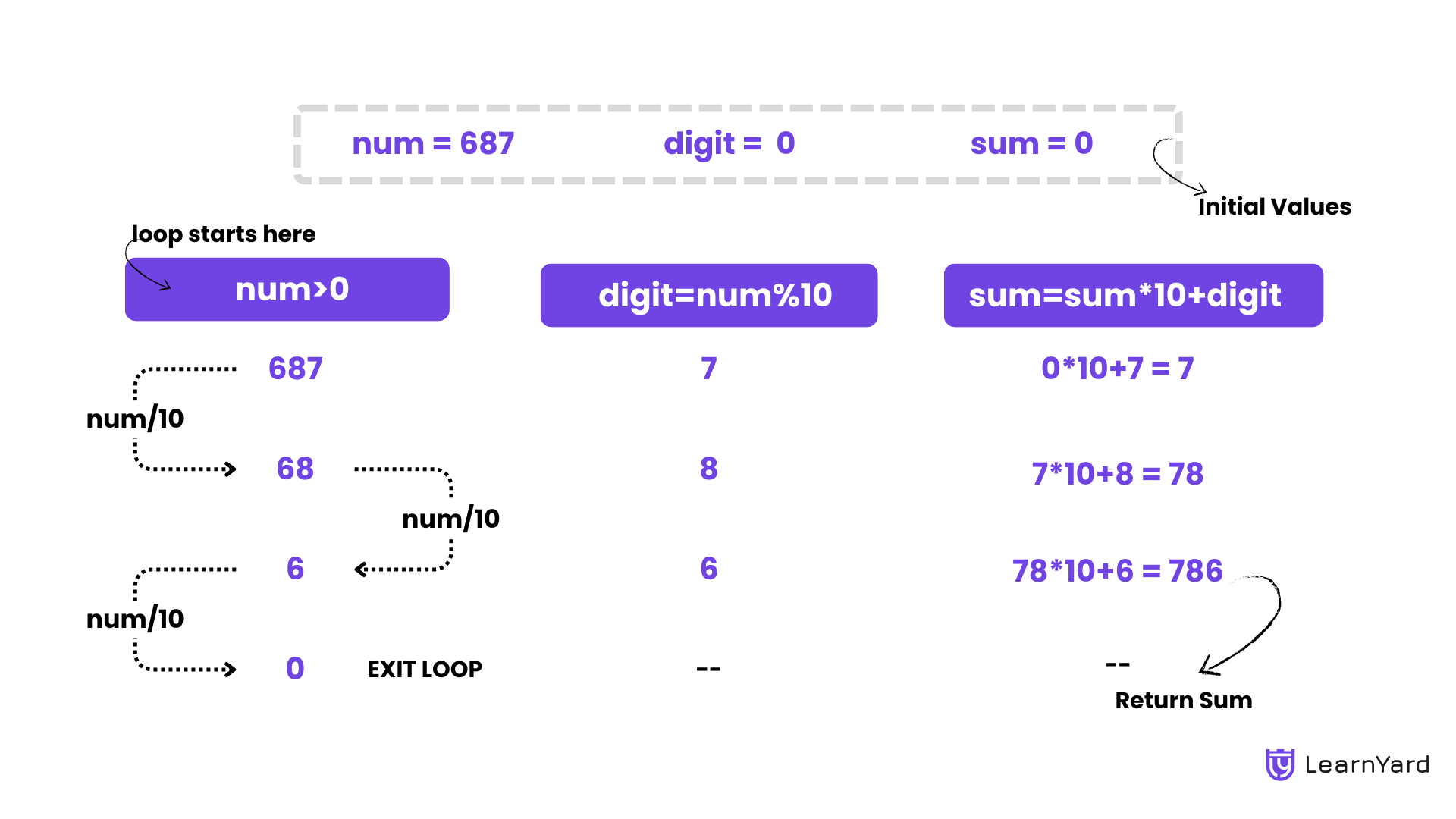
Let's understand it with an example for num = 12345
Initial values:
num = 12345
reversedNumber = 0
The number is in the decimal number system (Base 10).
First Iteration:
- Divide num by 10 → Quotient = 1234, Remainder = 5 (last digit of 12345).
- Update values:
- num = 1234
- reversedNumber = reversedNumber × 10 + 5 = 0 × 10 + 5 = 5
Second Iteration:
- Divide num by 10 → Quotient = 123, Remainder = 4 (last digit of 1234).
- Update values:
- num = 123
- reversedNumber = reversedNumber × 10 + 4 = 5 × 10 + 4 = 54
Third Iteration:
- Divide num by 10 → Quotient = 12, Remainder = 3 (last digit of 123).
- Update values:
- num = 12
- reversedNumber = reversedNumber × 10 + 3 = 54 × 10 + 3 = 543
Fourth Iteration:
- Divide num by 10 → Quotient = 1, Remainder = 2 (last digit of 12).
- Update values:
- num = 1
- reversedNumber = reversedNumber × 10 + 2 = 543 × 10 + 2 = 5432
Fifth Iteration:
- Divide num by 10 → Quotient = 0, Remainder = 1 (last digit of 1).
- Update values:
- num = 0
- reversedNumber = reversedNumber × 10 + 1 = 5432 × 10 + 1 = 54321
Loop Termination:
Now that num = 0, dividing it further will always return a quotient of 0 and a remainder of 0 infinitely. Since there is no sense in continuing the division, our loop should terminate.
and now we have reversedNumber = 54321.
Code Implementation
C++ Code Try on Compiler!
int reverseNumber(int num) {
int reversedNumber = 0;
while (num > 0) {
// Extract the last digit
int digit = num % 10;
// Build the reversed number
reversedNumber = reversedNumber * 10 + digit;
// Remove the last digit
num = num / 10;
}
return reversedNumber;
}Java Code Try on Compiler!
public class ReverseNumber {
public static int reverseNumber(int num) {
int reversedNumber = 0;
while (num > 0) {
int digit = num % 10;
reversedNumber = reversedNumber * 10 + digit;
num = num / 10;
}
return reversedNumber;
}
}
Python Code Try on Compiler!
def reverse_number(num):
reversed_number = 0
while num > 0:
digit = num % 10
reversed_number = reversed_number * 10 + digit
num = num // 10
return reversed_numberJavascript Code Try on Compiler!
function reverseNumber(num) {
let reversedNumber = 0;
while (num > 0) {
let digit = num % 10;
reversedNumber = reversedNumber * 10 + digit;
num = Math.floor(num / 10);
}
return reversedNumber;
}Time Complexity : O(logn)
The time complexity arises from the number of digits in the number. The number of times the while loop runs depends on the number of digits in the given number num.
For a given number num in a decimal representation, the number of digits is approximately equal to log10(num). This is because each digit represents a power of 10.
The loop executes once for each digit in num.
Therefore, the loop runs log10(num) times, which simplifies to O(logn).
Space Complexity : O(1)
We are using only variables like reversedNumber, and digits that use constant space.
Since the space required by these variables does not depend on the size of the input number num, the auxiliary space is O(1).
Now Since we have learned about how to reverse a number, let's solve another problem using the same concepts.
Similar Problems
Reverse bits of a given 32 bits unsigned integer.