Find the Minimum Area to Cover All Ones II Solution In C++/Python/java/JS
Find the Minimum Area to Cover All Ones II Problem
You are given a 2D binary array grid. You need to find 3 non-overlapping rectangles having non-zero areas with horizontal and vertical sides such that all the 1's in grid lie inside these rectangles.
Return the minimum possible sum of the area of these rectangles.
Note that the rectangles are allowed to touch.
Explanation
We are given a 2D binary matrix where each cell contains either 0 or 1. Our goal is to cover all the 1's in the matrix using exactly three non-overlapping rectangles. These rectangles must have non-zero areas and their sides must be aligned with the rows and columns of the matrix. The rectangles can touch each other but cannot overlap. Among all possible ways to place these rectangles, we need to find the configuration that results in the smallest total sum of their areas and return this minimum sum.
Example
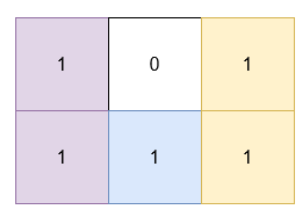
Input: grid = [[1,0,1],[1,1,1]]
Output: 5
Explanation:
The 1's at (0, 0) and (1, 0) are covered by a rectangle of area 2.
The 1's at (0, 2) and (1, 2) are covered by a rectangle of area 2.
The 1 at (1, 1) is covered by a rectangle of area 1.
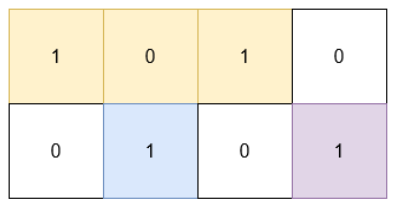
Input: grid = [[1,0,1,0],[0,1,0,1]]
Output: 5
Explanation:
The 1's at (0, 0) and (0, 2) are covered by a rectangle of area 3.
The 1 at (1, 1) is covered by a rectangle of area 1.
The 1 at (1, 3) is covered by a rectangle of area 1.
Constraints
- 1 <= grid.length, grid[i].length <= 30
- grid[i][j] is either 0 or 1.
- The input is generated such that there are at least three 1's in grid.
"Find the Minimum Area to Cover All Ones II" Problem requires a combination of enumeration and optimization to determine the best way to partition the grid into three non-overlapping rectangles. A brute force approach would be too slow, so we need to explore systematic ways to split the grid while minimizing the total area. By analyzing different configurations—horizontal splits, vertical splits, and mixed splits—we can efficiently determine the optimal arrangement. Let's break down the problem and explore the most effective approach!
Optimal Approach
Intuition
To solve this problem, we need to split the grid into three non-overlapping rectangles, ensuring that all 1’s are covered while keeping the total area as small as possible. These rectangles must be placed carefully to minimize wasted space, and we need to explore different ways to divide the grid efficiently.
Breaking It Down:
- We need three separate rectangles: Each rectangle should enclose some of the 1’s, and together, they must cover all 1’s in the grid.
- The rectangles cannot overlap: They can touch at edges but must remain separate.
"Our goal is to minimize the total area: The sum of the areas of these three rectangles should be as small as possible."
Understanding Through an Example
Imagine a grid like this:
[[0, 1, 1, 0],
[0, 1, 1, 0],
[1, 0, 0, 1],
[1, 0, 0, 1]]
- The 1’s are spread across different parts of the grid.
- We need to divide them into three non-overlapping rectangles.
- Our goal is to enclose all 1’s with the smallest total area.
Before diving into the problem, let's take a moment to sketch out different ways we can divide a rectangle into three separate rectangles. Here’s how we can break it down for any given rectangle.
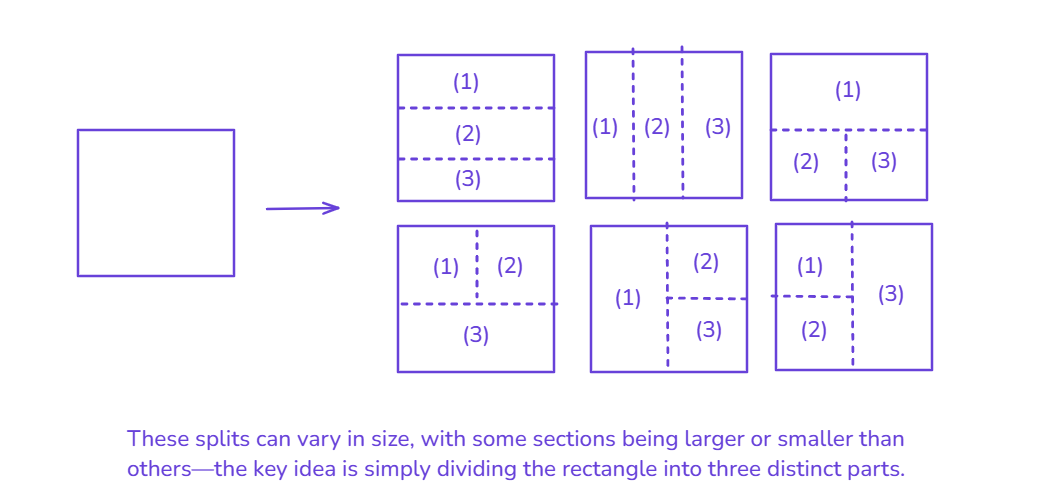
Now that we understand the different ways to divide a rectangle, let’s apply this idea to our grid and explore how we can split it effectively.
How Do We Approach This?
Explore different ways to split the grid:
Horizontal Splits: Divide the grid into three sections using two horizontal lines, meaning we try different row pairs to find the best split.
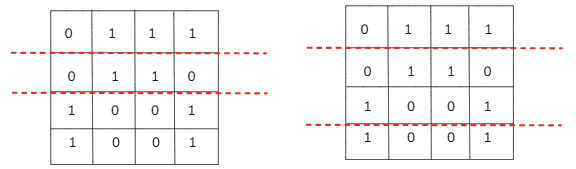
Vertical Splits: Similarly, divide the grid into three sections using two vertical lines, testing different column pairs for an optimal division.
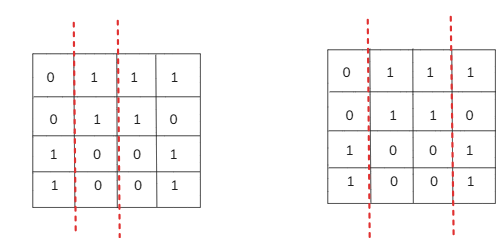
Combined Splits (Hybrid Approach): Instead of just horizontal or vertical cuts, we can first split in one direction and then further divide one of the sections in the other direction:
- Horizontal → Vertical: First, split the grid horizontally, then further divide either the top or bottom section vertically.
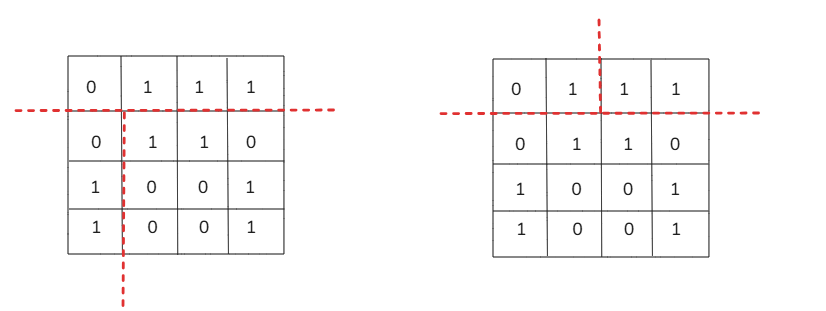
- Vertical → Horizontal: First, split the grid vertically, then further divide either the left or right section horizontally.
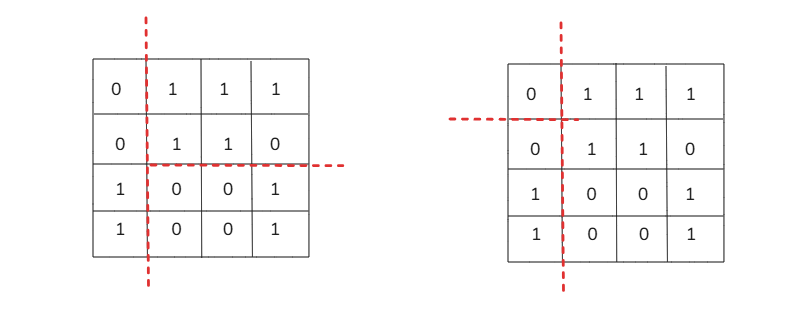
By trying all these possibilities, we can determine the minimum possible sum of the areas of the three rectangles that fully cover the 1.
Find the Minimum Area to Cover All Ones II Algorithm
- We initialize grid, rows, cols, and minArea.
- We iterate over possible horizontal splits, dividing the grid into three parts and computing their enclosing areas.
- We iterate over possible vertical splits, doing the same for columns.
- We explore four hybrid split cases, where we fix a row or column first, then split the remaining part.
- We compute the enclosing area for each subgrid using computeArea, which finds the smallest rectangle covering all 1s.
- We update minArea with the minimum sum of enclosing areas across all partitions.
- We return the final minArea as the result.
Approach
Initialize Grid and Variables
- The private instance variable grid is used to store the input grid.
- rows and cols are assigned the dimensions of the grid.
- minArea is initialized to rows * cols, representing the worst-case scenario.
Horizontal Splits
- Iterate over possible row pairs (firstRow, secondRow).
- Split the grid into three horizontal parts and compute their enclosing areas using computeArea().
- Update minArea with the minimum sum of these three areas.
Vertical Splits
- Iterate over possible column pairs (firstCol, secondCol).
- Split the grid into three vertical parts and compute their enclosing areas using computeArea().
- Update minArea accordingly.
Hybrid Splits
- Case 1: Fix a row, then try different column splits for the remaining part.
- Case 2: Fix a row in reverse order, then try different column splits.
- Case 3: Fix a column, then try different row splits for the remaining part.
- Case 4: Fix a column in reverse order, then try different row splits.
For each case, compute the enclosing areas and update minArea.
Compute Enclosing Area
- Finds the smallest bounding rectangle for 1s in a given subgrid.
- Iterates over the subgrid to track the minimum and maximum row/column indices where 1s appear.
- Returns the area of the enclosing rectangle as (maxRow - minRow + 1) * (maxCol - minCol + 1).
Return the Minimum Area Sum
- After evaluating all possible splits, the smallest sum of enclosing areas across all partitions is returned as the result.
Dry-Run
Example
Input:
grid = [[1, 0, 0],
[1, 1, 0],
[0, 1, 1]]
Output: 5 →
Explanation:
1. Initialize Variables
- rows = 3, cols = 3
- minArea = 9 (maximum possible grid size)
- Store grid in private int[][] grid.
2. Check Possible Splits and Compute Areas
Horizontal Splits (Splitting Grid into Three Horizontal Parts)
Split at (Row 0, Row 1, Row 2)
- Part 1 (Top Subgrid: Rows 0 to 0)
→ [1, 0, 0]
→ Bounding Box of 1s: (0,0) → (0,0)
→ Area = (0-0+1) * (0-0+1) = 1 - Part 2 (Middle Subgrid: Rows 1 to 1)
→ [1, 1, 0]
→ Bounding Box of 1s: (1,0) → (1,1)
→ Area = (1-1+1) * (1-0+1) = 2 - Part 3 (Bottom Subgrid: Rows 2 to 2)
→ [0, 1, 1]
→ Bounding Box of 1s: (2,1) → (2,2)
→ Area = (2-2+1) * (2-1+1) = 2 - Total Area = 1 + 2 + 2 = 5
→ Update minArea = 5 (smaller than 9)
Vertical Splits (Splitting Grid into Three Vertical Parts)
Split at (Col 0, Col 1, Col 2)
- Part 1 (Left Subgrid: Cols 0 to 0)
→ [[1], [1], [0]]
→ Bounding Box of 1s: (0,0) → (1,0)
→ Area = (1-0+1) * (0-0+1) = 2 - Part 2 (Middle Subgrid: Cols 1 to 1)
→ [[0], [1], [1]]
→ Bounding Box of 1s: (1,1) → (2,1)
→ Area = (2-1+1) * (1-1+1) = 2 - Part 3 (Right Subgrid: Cols 2 to 2)
→ [[0], [0], [1]]
→ Bounding Box of 1s: (2,2) → (2,2)
→ Area = (2-2+1) * (2-2+1) = 1 - Total Area = 2 + 2 + 1 = 5
→ minArea remains 5
Hybrid Splits (Left-Right, then Top-Bottom on Right)
Example Split:
Left Part (Cols 0 to 0, Full Rows) ⇒
· [[1], [1], [0]]
· Bounding Box of 1s: (0,0) → (1,0)
· Area = 2
Right Part (Cols 1 to 2, Split into Top and Bottom)
· Top Part (Row 0)
· [0, 0]
· No 1s → Area = 0
Bottom Part (Rows 1-2)
· [[1, 0], [1, 1]]
· Bounding Box of 1s: (1,1) → (2,2)
· Area = (2-1+1) * (2-1+1) = 4
Total Area = 2 + 0 + 4 = 6
· minArea remains 5 (smaller than 6)
3. Return minArea
- Final Minimum Enclosing Area = 5
- Output: 5
Optimal Code in all Languages
1. Find the Minimum Area to Cover All Ones II solution in C++ Try on Compiler
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
class Solution {
private:
vector<vector<int>> grid;
// Helper method to compute the minimum area enclosing all 1s in a subgrid
int computeArea(int topRow, int leftCol, int bottomRow, int rightCol) {
int minRow = INT_MAX, minCol = INT_MAX;
int maxRow = INT_MIN, maxCol = INT_MIN;
// Iterate over the subgrid to find the bounding rectangle for cells with value 1
for (int i = topRow; i <= bottomRow; i++) {
for (int j = leftCol; j <= rightCol; j++) {
if (grid[i][j] == 1) {
minRow = min(minRow, i);
minCol = min(minCol, j);
maxRow = max(maxRow, i);
maxCol = max(maxCol, j);
}
}
}
if (minRow == INT_MAX) return 0; // No '1' found in the subgrid
return (maxRow - minRow + 1) * (maxCol - minCol + 1);
}
public:
int minimumSum(vector<vector<int>>& grid) {
this->grid = grid;
int rows = grid.size();
int cols = grid[0].size();
int minArea = rows * cols;
// Horizontal splits
for (int firstRow = 0; firstRow < rows - 1; firstRow++) {
for (int secondRow = firstRow + 1; secondRow < rows - 1; secondRow++) {
int currentArea = computeArea(0, 0, firstRow, cols - 1) +
computeArea(firstRow + 1, 0, secondRow, cols - 1) +
computeArea(secondRow + 1, 0, rows - 1, cols - 1);
minArea = min(minArea, currentArea);
}
}
// Vertical splits
for (int firstCol = 0; firstCol < cols - 1; firstCol++) {
for (int secondCol = firstCol + 1; secondCol < cols - 1; secondCol++) {
int currentArea = computeArea(0, 0, rows - 1, firstCol) +
computeArea(0, firstCol + 1, rows - 1, secondCol) +
computeArea(0, secondCol + 1, rows - 1, cols - 1);
minArea = min(minArea, currentArea);
}
}
// Hybrid splits - Case 1
for (int row = 0; row < rows - 1; row++) {
int firstArea = computeArea(0, 0, row, cols - 1);
for (int col = 0; col < cols - 1; col++) {
int secondArea = computeArea(row + 1, 0, rows - 1, col);
int thirdArea = computeArea(row + 1, col + 1, rows - 1, cols - 1);
minArea = min(minArea, firstArea + secondArea + thirdArea);
}
}
// Hybrid splits - Case 2
for (int row = rows - 1; row >= 0; row--) {
int firstArea = computeArea(row + 1, 0, rows - 1, cols - 1);
for (int col = 0; col < cols - 1; col++) {
int secondArea = computeArea(0, 0, row, col);
int thirdArea = computeArea(0, col + 1, row, cols - 1);
minArea = min(minArea, firstArea + secondArea + thirdArea);
}
}
// Hybrid splits - Case 3
for (int col = 0; col < cols - 1; col++) {
int firstArea = computeArea(0, 0, rows - 1, col);
for (int row = 0; row < rows - 1; row++) {
int secondArea = computeArea(0, col, row, cols - 1);
int thirdArea = computeArea(row + 1, col, rows - 1, cols - 1);
minArea = min(minArea, firstArea + secondArea + thirdArea);
}
}
// Hybrid splits - Case 4
for (int col = cols - 1; col >= 0; col--) {
int firstArea = computeArea(0, col + 1, rows - 1, cols - 1);
for (int row = 0; row < rows - 1; row++) {
int secondArea = computeArea(0, 0, row, col);
int thirdArea = computeArea(row + 1, 0, rows - 1, col);
minArea = min(minArea, firstArea + secondArea + thirdArea);
}
}
return minArea;
}
};
int main() {
int rows, cols;
cin >> rows >> cols;
vector<vector<int>> grid(rows, vector<int>(cols));
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
cin >> grid[i][j];
}
}
Solution solution;
cout << solution.minimumSum(grid) << endl;
return 0;
}
2. Find the Minimum Area to Cover All Ones II solution in Java Try on Compiler
import java.util.*;
class Solution {
private int[][] grid;
public int minimumSum(int[][] grid) {
this.grid = grid;
int rows = grid.length;
int cols = grid[0].length;
int minArea = rows * cols;
// Horizontal splits
for (int firstRow = 0; firstRow < rows - 1; firstRow++) {
for (int secondRow = firstRow + 1; secondRow < rows - 1; secondRow++) {
int currentArea = computeArea(0, 0, firstRow, cols - 1) +
computeArea(firstRow + 1, 0, secondRow, cols - 1) +
computeArea(secondRow + 1, 0, rows - 1, cols - 1);
minArea = Math.min(minArea, currentArea);
}
}
// Vertical splits
for (int firstCol = 0; firstCol < cols - 1; firstCol++) {
for (int secondCol = firstCol + 1; secondCol < cols - 1; secondCol++) {
int currentArea = computeArea(0, 0, rows - 1, firstCol) +
computeArea(0, firstCol + 1, rows - 1, secondCol) +
computeArea(0, secondCol + 1, rows - 1, cols - 1);
minArea = Math.min(minArea, currentArea);
}
}
// Hybrid splits - Case 1
for (int row = 0; row < rows - 1; row++) {
int firstArea = computeArea(0, 0, row, cols - 1);
for (int col = 0; col < cols - 1; col++) {
int secondArea = computeArea(row + 1, 0, rows - 1, col);
int thirdArea = computeArea(row + 1, col + 1, rows - 1, cols - 1);
minArea = Math.min(minArea, firstArea + secondArea + thirdArea);
}
}
// Hybrid splits - Case 2
for (int row = rows - 1; row >= 0; row--) {
int firstArea = computeArea(row + 1, 0, rows - 1, cols - 1);
for (int col = 0; col < cols - 1; col++) {
int secondArea = computeArea(0, 0, row, col);
int thirdArea = computeArea(0, col + 1, row, cols - 1);
minArea = Math.min(minArea, firstArea + secondArea + thirdArea);
}
}
// Hybrid splits - Case 3
for (int col = 0; col < cols - 1; col++) {
int firstArea = computeArea(0, 0, rows - 1, col);
for (int row = 0; row < rows - 1; row++) {
int secondArea = computeArea(0, col, row, cols - 1);
int thirdArea = computeArea(row + 1, col, rows - 1, cols - 1);
minArea = Math.min(minArea, firstArea + secondArea + thirdArea);
}
}
// Hybrid splits - Case 4
for (int col = cols - 1; col >= 0; col--) {
int firstArea = computeArea(0, col + 1, rows - 1, cols - 1);
for (int row = 0; row < rows - 1; row++) {
int secondArea = computeArea(0, 0, row, col);
int thirdArea = computeArea(row + 1, 0, rows - 1, col);
minArea = Math.min(minArea, firstArea + secondArea + thirdArea);
}
}
return minArea;
}
// Helper method to compute the minimum area enclosing all 1s in a subgrid
public int computeArea(int topRow, int leftCol, int bottomRow, int rightCol) {
int minRow = Integer.MAX_VALUE, minCol = Integer.MAX_VALUE;
int maxRow = Integer.MIN_VALUE, maxCol = Integer.MIN_VALUE;
// Iterate over the subgrid to find the bounding rectangle for cells with value 1
for (int i = topRow; i <= bottomRow; i++) {
for (int j = leftCol; j <= rightCol; j++) {
if (grid[i][j] == 1) {
minRow = Math.min(minRow, i);
minCol = Math.min(minCol, j);
maxRow = Math.max(maxRow, i);
maxCol = Math.max(maxCol, j);
}
}
}
return (maxRow - minRow + 1) * (maxCol - minCol + 1);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int rows = scanner.nextInt();
int cols = scanner.nextInt();
int[][] grid = new int[rows][cols];
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
grid[i][j] = scanner.nextInt();
}
}
scanner.close();
Solution solution = new Solution();
System.out.println(solution.minimumSum(grid));
}
}
3. Find the Minimum Area to Cover All Ones I solution in Python Try on Compiler
from typing import List
class Solution:
def __init__(self):
self.grid = [] # Private grid variable
def minimumSum(self, grid: List[List[int]]) -> int:
self.grid = grid # Store the grid
rows, cols = len(grid), len(grid[0])
min_area = rows * cols # Initialize with maximum possible area
# Horizontal splits
for first_row in range(rows - 1):
for second_row in range(first_row + 1, rows - 1):
current_area = (self.computeArea(0, 0, first_row, cols - 1) +
self.computeArea(first_row + 1, 0, second_row, cols - 1) +
self.computeArea(second_row + 1, 0, rows - 1, cols - 1))
min_area = min(min_area, current_area)
# Vertical splits
for first_col in range(cols - 1):
for second_col in range(first_col + 1, cols - 1):
current_area = (self.computeArea(0, 0, rows - 1, first_col) +
self.computeArea(0, first_col + 1, rows - 1, second_col) +
self.computeArea(0, second_col + 1, rows - 1, cols - 1))
min_area = min(min_area, current_area)
# Hybrid splits - Case 1
for row in range(rows - 1):
first_area = self.computeArea(0, 0, row, cols - 1)
for col in range(cols - 1):
second_area = self.computeArea(row + 1, 0, rows - 1, col)
third_area = self.computeArea(row + 1, col + 1, rows - 1, cols - 1)
min_area = min(min_area, first_area + second_area + third_area)
# Hybrid splits - Case 2
for row in range(rows - 1, -1, -1):
first_area = self.computeArea(row + 1, 0, rows - 1, cols - 1)
for col in range(cols - 1):
second_area = self.computeArea(0, 0, row, col)
third_area = self.computeArea(0, col + 1, row, cols - 1)
min_area = min(min_area, first_area + second_area + third_area)
# Hybrid splits - Case 3
for col in range(cols - 1):
first_area = self.computeArea(0, 0, rows - 1, col)
for row in range(rows - 1):
second_area = self.computeArea(0, col, row, cols - 1)
third_area = self.computeArea(row + 1, col, rows - 1, cols - 1)
min_area = min(min_area, first_area + second_area + third_area)
# Hybrid splits - Case 4
for col in range(cols - 1, -1, -1):
first_area = self.computeArea(0, col + 1, rows - 1, cols - 1)
for row in range(rows - 1):
second_area = self.computeArea(0, 0, row, col)
third_area = self.computeArea(row + 1, 0, rows - 1, col)
min_area = min(min_area, first_area + second_area + third_area)
return min_area
def computeArea(self, top_row: int, left_col: int, bottom_row: int, right_col: int) -> int:
min_row, min_col = float('inf'), float('inf')
max_row, max_col = float('-inf'), float('-inf')
# Iterate over the subgrid to find the bounding rectangle for cells with value 1
for i in range(top_row, bottom_row + 1):
for j in range(left_col, right_col + 1):
if self.grid[i][j] == 1:
min_row, min_col = min(min_row, i), min(min_col, j)
max_row, max_col = max(max_row, i), max(max_col, j)
return (max_row - min_row + 1) * (max_col - min_col + 1) if min_row != float('inf') else 0
# Input Handling
def main():
rows, cols = map(int, input().split())
grid = [list(map(int, input().split())) for _ in range(rows)]
solution = Solution()
print(solution.minimumSum(grid))
if __name__ == "__main__":
main()
4. Find the Minimum Area to Cover All Ones I solution in JavaScript Try on Compiler
const fs = require("fs");
/**
* @param {number[][]} grid
* @return {number}
*/
var minimumSum = function(grid) {
this.grid = grid;
const rows = grid.length;
const cols = grid[0].length;
let minArea = rows * cols;
// Function to compute the minimum area enclosing all 1s in a subgrid
function computeArea(topRow, leftCol, bottomRow, rightCol) {
let minRow = Infinity, minCol = Infinity;
let maxRow = -Infinity, maxCol = -Infinity;
for (let i = topRow; i <= bottomRow; i++) {
for (let j = leftCol; j <= rightCol; j++) {
if (grid[i][j] === 1) {
minRow = Math.min(minRow, i);
minCol = Math.min(minCol, j);
maxRow = Math.max(maxRow, i);
maxCol = Math.max(maxCol, j);
}
}
}
return (maxRow - minRow + 1) * (maxCol - minCol + 1);
}
// Horizontal splits
for (let firstRow = 0; firstRow < rows - 1; firstRow++) {
for (let secondRow = firstRow + 1; secondRow < rows - 1; secondRow++) {
let currentArea = computeArea(0, 0, firstRow, cols - 1) +
computeArea(firstRow + 1, 0, secondRow, cols - 1) +
computeArea(secondRow + 1, 0, rows - 1, cols - 1);
minArea = Math.min(minArea, currentArea);
}
}
// Vertical splits
for (let firstCol = 0; firstCol < cols - 1; firstCol++) {
for (let secondCol = firstCol + 1; secondCol < cols - 1; secondCol++) {
let currentArea = computeArea(0, 0, rows - 1, firstCol) +
computeArea(0, firstCol + 1, rows - 1, secondCol) +
computeArea(0, secondCol + 1, rows - 1, cols - 1);
minArea = Math.min(minArea, currentArea);
}
}
// Hybrid splits
for (let row = 0; row < rows - 1; row++) {
let firstArea = computeArea(0, 0, row, cols - 1);
for (let col = 0; col < cols - 1; col++) {
let secondArea = computeArea(row + 1, 0, rows - 1, col);
let thirdArea = computeArea(row + 1, col + 1, rows - 1, cols - 1);
minArea = Math.min(minArea, firstArea + secondArea + thirdArea);
}
}
return minArea;
};
// Read input using fs.readFileSync
const input = fs.readFileSync(0, "utf8").trim().split("\n");
const [rows, cols] = input[0].split(" ").map(Number);
const grid = input.slice(1).map(line => line.split(" ").map(Number));
console.log(minimumSum(grid));
Time Complexity: O(m^2 x n^2)
This approach efficiently finds the minimum area enclosing all 1s by evaluating different possible splits in the grid. Below is the detailed breakdown:
1. Horizontal and Vertical Splits:
→ The loops for horizontal splits run m times for the outer loop and m times for the inner loop, resulting in O(m^2).
→ Similarly, the loops for vertical splits run n times for the outer loop and n times for the inner loop, resulting in O(n^2).
→ Each iteration of these loops calls the computeArea method three times, which has a time complexity of O(m × n).
2. Hybrid Splits:
→ For each of the four hybrid split cases, the outer loops run m times or n times, and the inner loops run n times or m times, resulting in O(m × n) for each hybrid split case.
→ Each iteration of these loops also calls the computeArea method three times, which has a time complexity of O(m × n).
Overall Time Complexity: Combining these complexities, the overall time complexity of the minimumSum method is:
O(m^2 × n + n^2 × m + m × n × (m + n))
Simplifying this, we get:
O(m^2 × n + n^2 × m) = O(m^2 x n^2)
Space Complexity: O(m x n)
Auxiliary Space Complexity refers to extra space used beyond the input grid. In this approach, we store the grid as a class-level variable in Java, C++, Python, and JavaScript implementations, but it does not contribute extra space. The only extra space used is for loop variables and function call stack, which is O(1).
Total Space Complexity
The total space includes only the input grid of O(m × n) space. No additional storage (such as new matrices or arrays) is used beyond the input grid.
Thus, the overall space complexity is O(m × n).
Similar Problems
Now, since we have figured out the Robot Collisions solution, let's try out similar problems of "".
You are given a 2D binary array grid. You need to find 3 non-overlapping rectangles having non-zero areas with horizontal and vertical sides such that all the 1's in grid lie inside these rectangles.
Return the minimum possible sum of the area of these rectangles.
Note that the rectangles are allowed to touch.