Find Sum and Product of All the Elements in an Array Solution in C++/Java/Python/JS

As we progress in this discussion, we often need to perform operations such as finding the collective sum, product, or any other operation such as (GCD, or applying bitwise operations) on the entire array. Let’s now explore how these tasks can be accomplished. Since sum and product are the basic ones, we will discuss those here.
Write a program that takes an array as input and calculates both the sum and the product of all the elements in the array.
Example
Input: nums = [1, 2, 3, 4]
Output:
Sum: 10
Product: 24
Explanation: The sum of the elements (1 + 2 + 3 + 4) is 10, and the product (1 * 2 * 3 * 4) is 24.
Input: nums = [5, 6, 7]
Output:
Sum: 18
Product: 210
Explanation: The sum of the elements (5 + 6 + 7) is 18, and the product (5 * 6 * 7) is 210.
Approach
To solve the problem of finding the sum and product of all elements in an array, we need to focus on two main tasks: adding the values of all elements together to get the sum, and multiplying the values of all elements together to get the product.
Imagine you have a list of numbers, and you want to know two things:
- What is the total when you add all the numbers together?
- What is the result when you multiply all the numbers together?
For example, if you have numbers [2, 3, 4], you would want to:
- Add them: 2 + 3 + 4 = 9
- Multiply them: 2 * 3 * 4 = 24
To keep track of the sum and product as we go through the list, we use two variables:
- sum will start at 0 because adding 0 to any number doesn't change the number.
- product will start at 1 because multiplying by 1 doesn’t change the number.
We will use a loop to go through each number in the array. As we encounter each number:
- Add the number to our sum variable. (sum += nums[index])
- Multiply the number with our product variable. (product *= nums[index])
Once we’ve gone through the entire array, sum will hold the total sum of all the numbers, and product will hold the total product of all the numbers.
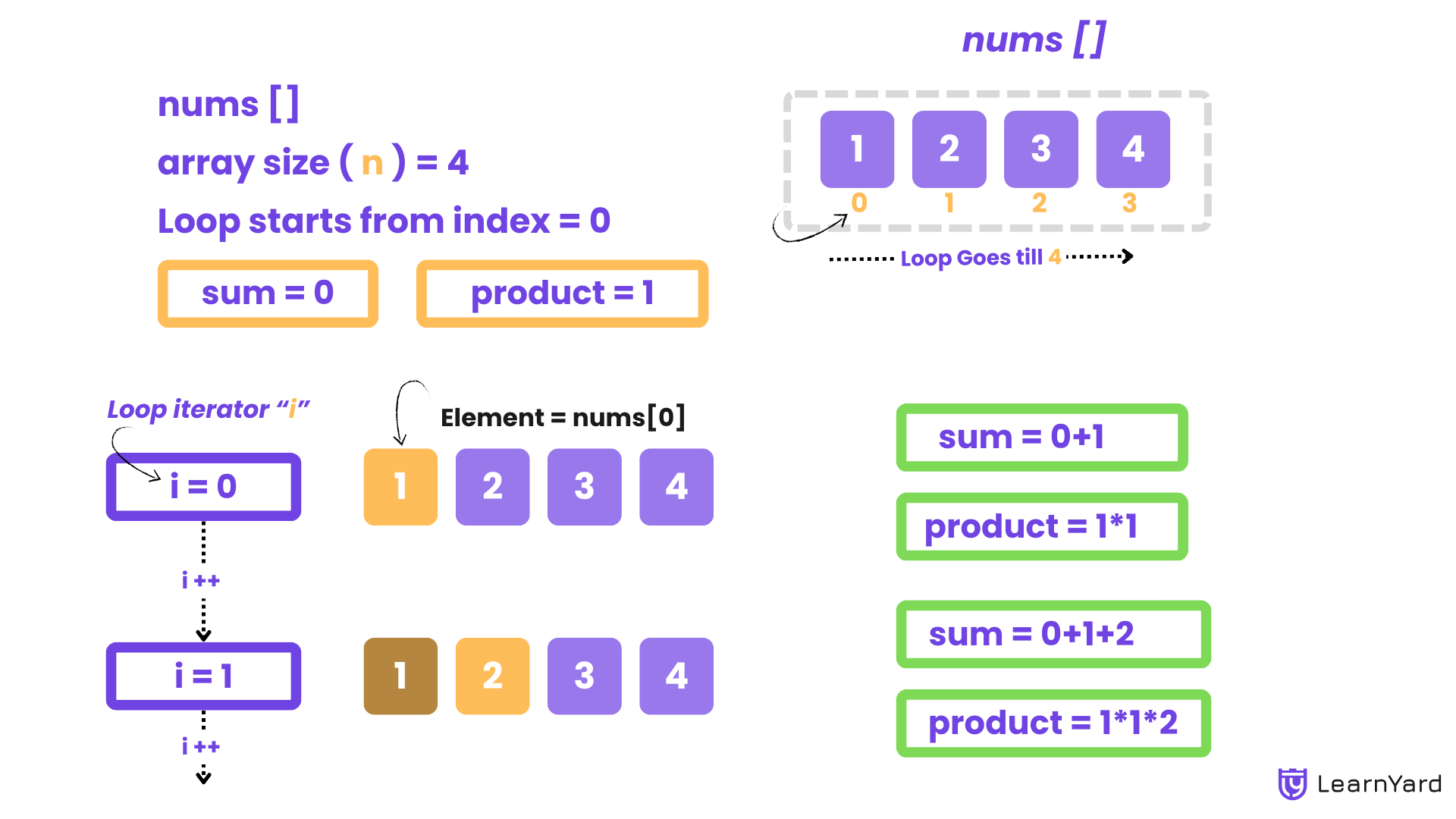
Dry Run
Input: nums = [1, 2, 3, 4]
- Initialization:
- sum = 0
- product = 1
- First Iteration (index = 0):
- Current number = 1
- sum = sum + 1 = 0 + 1 = 1
- product = product * 1 = 1 * 1 = 1
- Second Iteration (index = 1):
- Current number = 2
- sum = sum + 2 = 1 + 2 = 3
- product = product * 2 = 1 * 2 = 2
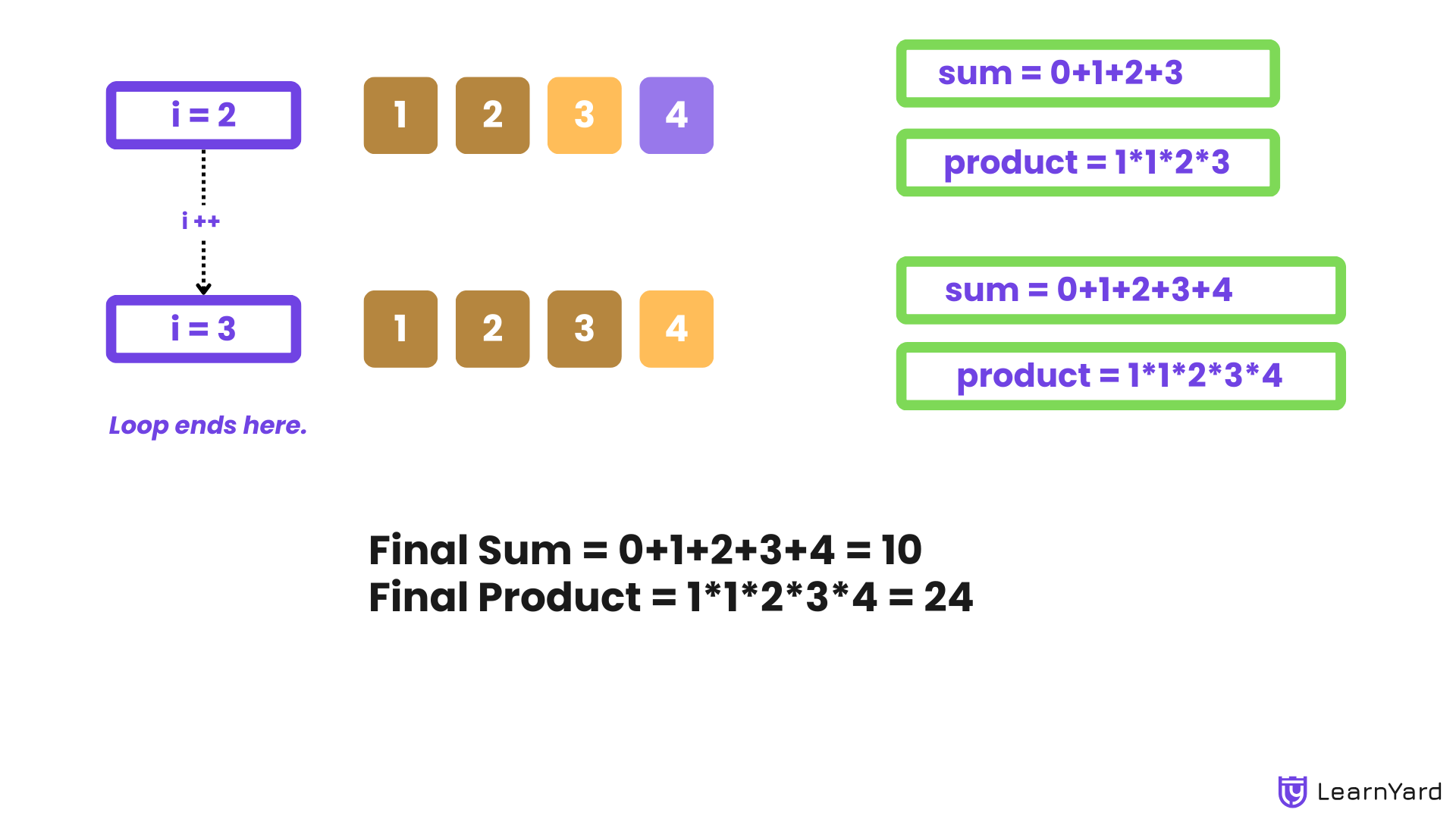
- Third Iteration (index = 2):
- Current number = 3
- sum = sum + 3 = 3 + 3 = 6
- product = product * 3 = 2 * 3 = 6
- Fourth Iteration (index = 3):
- Current number = 4
- sum = sum + 4 = 6 + 4 = 10
- product = product * 4 = 6 * 4 = 24
- Output:
- Sum: 10
- Product: 24
Code for All Languages
C++
#include <iostream>
using namespace std;
// Function to calculate the sum and product of the array
void calculateSumAndProduct(int nums[], int size) {
// Initialize variables to store the sum and product
int sum = 0;
int product = 1;
// Loop through the array to calculate the sum and product
for (int index = 0; index < size; ++index) {
// Add the value at the current index to the sum
sum += nums[index];
// Multiply the value at the current index to the product
product *= nums[index];
}
// Print the calculated sum
cout << "Sum: " << sum << endl;
// Print the calculated product
cout << "Product: " << product << endl;
}Java
import java.util.Scanner;
public class LearnYard {
// Function to calculate the sum and product of the array
public static void calculateSumAndProduct(int[] nums, int size) {
// Initialize variables to store the sum and product
int sum = 0;
int product = 1;
// Loop through the array to calculate the sum and product
for (int index = 0; index < size; ++index) {
// Add the value at the current index to the sum
sum += nums[index];
// Multiply the value at the current index to the product
product *= nums[index];
}
// Print the calculated sum
System.out.println("Sum: " + sum);
// Print the calculated product
System.out.println("Product: " + product);
}
}Python
# Function to calculate the sum and product of the array
def calculate_sum_and_product(nums):
# Initialize variables to store the sum and product
sum = 0
product = 1
# Loop through the array to calculate the sum and product
for num in nums:
# Add the current number to the sum
sum += num
# Multiply the current number to the product
product *= num
# Print the calculated sum
print("Sum:", sum)
# Print the calculated product
print("Product:", product)Javascript
// Function to calculate the sum and product of the array
function calculateSumAndProduct(nums) {
// Initialize variables to store the sum and product
let sum = 0;
let product = 1;
// Loop through the array to calculate the sum and product
for (let i = 0; i < nums.length; i++) {
// Add the current number to the sum
sum += nums[i];
// Multiply the current number to the product
product *= nums[i];
}
// Print the calculated sum
console.log("Sum:", sum);
// Print the calculated product
console.log("Product:", product);
}
Time Complexity: O(n)
Here, n is the number of elements in the array. The loop iterates through each element in the array exactly once, performing a constant-time operation (addition and multiplication) for each element. Therefore, the time complexity is linear, or O(n).
Space Complexity: O(1)
Auxiliary Space Complexity: This refers to any extra space used by the algorithm that is independent of the input space and output space. In this case, we only use a constant amount of extra space, specifically for the variables. These variables do not depend on the size of the array and therefore take up constant space. so the auxiliary space complexity is O(1).
Total Space Complexity: This includes the space required for the input, output and extra space used by the algorithm as well. The input array nums[] is of size n, So the space required for input space is O(n). No output space is used. Also, the algorithm takes only constant extra space.
Total Space Complexity = O(n) + O(1) + O(1) = O(n)