How to Calculate?

To calculate Time Complexity, we must try to understand the code line-by-line and see how many operations it will have to do for a given set of inputs. After finding the approximate number of operations as a function of the input variable:

1. Get rid of those terms that will become insignificant compared to the most significant term, when the values of the terms tend to be very large.
2. Ignore the constants you see with the most significant term; here, you have your desired time complexity.

Now, what could be a question mark in your head is what is meant by an operation. On a high level, things like array accesses, additions, bit-shifts, multiplies, subtractions, xors, taking an input of an integer/float, printing an integer, etc., are what I mean by an operation.

Let's take a simple (or maybe not-so-simple) example to understand.

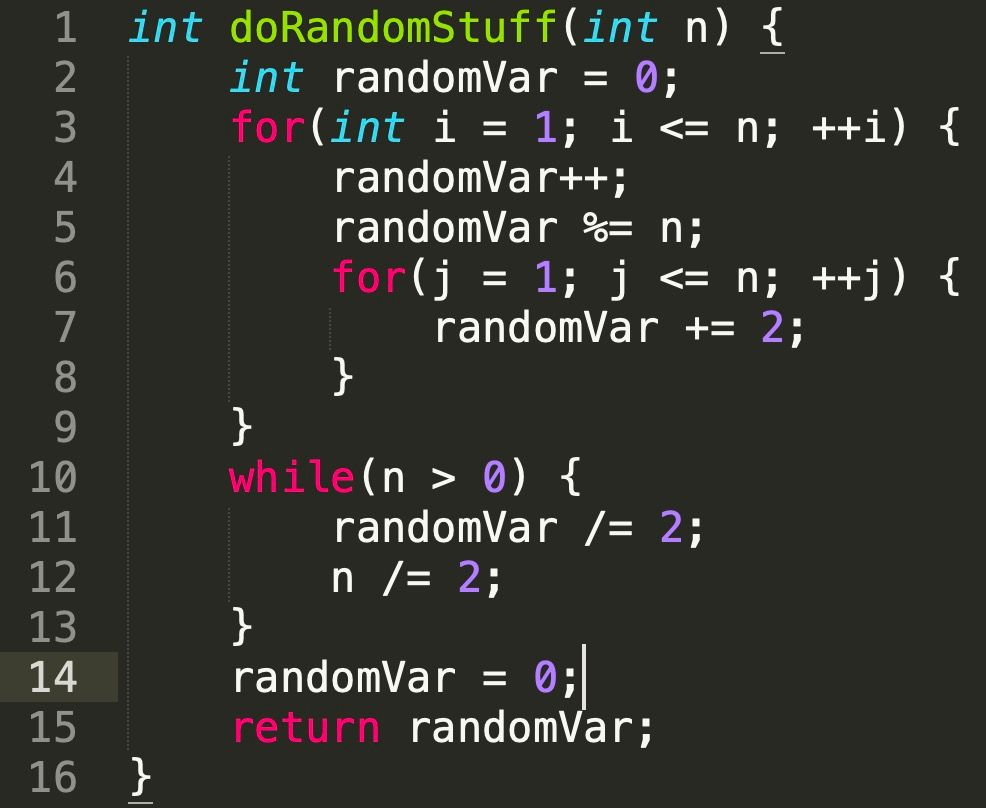
In the code snippet above:

1. The code on Line 2 runs just once, so one operation.
2. Lines 4 & 5 run n times, so 2*n more operations.
3. Line 7 runs n² times, so n² more operations.
4. Then, for lines 11 & 12, notice that n is divided by 2 in each iteration, which means that the while loop will run approximately log₂n times; therefore, 2*log₂n more operations.
5. Finally, lines 14 & 15 run once, so two last operations.

Adding all of these up:

total_operations = n² + 2n + 2log₂n + 3 (approximately)

1. Get rid of the terms that don't match the most significant term's growth rate. We'll be left with just n²
2. Now, n² has no constant with it to get rid of.
3. Here we go; the final time complexity is O(N²).

Note: Calculating time complexity is not always a very trivial task, sometimes we may think that a line of code runs X number of times, but when looked closely it may not be the case.

But well, practice, and you'll become better at it.