Arrays: Practice Problems IV
Hey! So, we have finally reached to the last article of arrays practice.
Excited about the same? Let's conquer it together!
Problem 1: Write a java program to merge two sorted array to third array.
Input
Array 1: 1, 4, 6, 9, 15
Array 2: 2, 5, 8, 10Output
1, 2, 4, 5, 6, 8, 9, 10, 15Approach
Explanation/Steps
The arrays can be merged as follows:
- Make an array of size equal to the sum of the sizes of arrays 1 and 2.
- Initialize two pointers. One points to the beginning of array 1, while the other points to the beginning of array 2.
- Now we'll compare the values of the elements to which the pointers point.
If the element of array1 is smaller than the element of array2, we will add it to the final merged array and move pointer1 up one position.
Otherwise, we will add the element from array2 to the final merged array and increment the position of pointer2 by one. - And so on, we will compare value of pointer1 and pointer2 until we reach the end of atleast one array.
- Finally we will append the elements left in either of the arrays to the merged array. That's it!
Solution
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// Input size of first array
Scanner scanner = new Scanner(System.in);
System.out.println("Enter the size of the first array: ");
int size1 = scanner.nextInt();
int[] arr1 = new int[size1];
// Input elements in the first array
System.out.println("Enter elements in the first array: ");
for (int i = 0; i < size1; i++) {
arr1[i] = scanner.nextInt();
}
// Input size of the second array
System.out.println("Enter the size of the second array: ");
int size2 = scanner.nextInt();
int[] arr2 = new int[size2];
// Input elements in the second array
System.out.println("Enter elements in the second array: ");
for (int i = 0; i < size2; i++) {
arr2[i] = scanner.nextInt();
}
// Creating the mergedArray
int mergeSize = size1 + size2;
int[] mergeArray = new int[mergeSize];
// Merge two arrays in ascending order
int index1 = 0;
int index2 = 0;
int mergeIndex = 0;
while (index1 < size1 && index2 < size2) {
// If element of array1 is smaller than element of array2,
// we will consider it
if (arr1[index1] < arr2[index2]) {
mergeArray[mergeIndex] = arr1[index1];
index1++;
}
// Otherwise we will consider element of array2
else {
mergeArray[mergeIndex] = arr2[index2];
index2++;
}
mergeIndex++;
}
// Merge remaining array elements
while (index1 < size1) {
mergeArray[mergeIndex] = arr1[index1];
mergeIndex++;
index1++;
}
while (index2 < size2) {
mergeArray[mergeIndex] = arr2[index2];
mergeIndex++;
index2++;
}
// Print merged array
System.out.println("Array merged in ascending order: ");
for (int i = 0; i < mergeSize; i++) {
System.out.print(mergeArray[i] + "\t");
}
System.out.println();
scanner.close();
}
}Problem 2: Write a java program to reverse the elements of an array.
Input
5
10, 5, 16, 35, 500Output
500, 35, 16, 5, 10Approach
Explanation/Steps
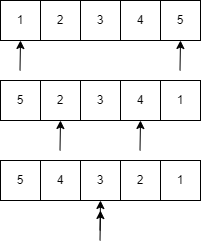
- Iterate through the array using 2 pointers. One pointer pointing to the start of the array moving in the forward direction. Another pointing to the end of the array moving in backward direction.
- Swap elements pointed by the pointers. And move the first pointer towards end and the last pointer towards start.
- Do this until they meet or cross each other.
Solution
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// Input size of array
Scanner scanner = new Scanner(System.in);
System.out.println("Enter size of the array: ");
int size = scanner.nextInt();
int[] arr = new int[size];
// Input array elements
System.out.println("Enter elements in array: ");
for (int i = 0; i < size; i++) {
arr[i] = scanner.nextInt();
}
// Reversing the array using 2 pointers
int start = 0, end = size - 1;
while(start < end){
int temp = arr[start];
arr[start++] = arr[end];
arr[end--] = temp;
}
// Print array in reversed order
System.out.println("Reversed array: ");
for (int i = 0; i < size; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
scanner.close();
}
}
Problem 3: Write a java program to search element in an array.
Input consists of elements of array and the element to be searched. If the array consists the element, return its index otherwise return -1.
Input
Size of array: 10
Elements of array: 10, 12, 20, 25, 13, 10, 9, 40, 60, 5
Element to search: 25Output
3Approach
Explanation/Steps
- Maintain a variable "searchIdx" to store the index of element to be searched if found. We initialize it with -1, in order to check after traversal, if element was there in array or not.
- Traverse the array, checking for the element to be searched. If found, update the value of searchIdx with the current index and break.
- Finally, if the "searchIdx" is equal to -1 even after traversal, that means we could not find the element in the array, so print that. Else print the value of "searchIdx".
Solution
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// Input size of array
Scanner scanner = new Scanner(System.in);
System.out.println("Enter size of array: ");
int size = scanner.nextInt();
int[] arr = new int[size];
// Input elements of array
System.out.println("Enter elements in array: ");
for (int i = 0; i < size; i++) {
arr[i] = scanner.nextInt();
}
System.out.println("Enter element to search: ");
int toSearch = scanner.nextInt();
// Assume that element does not exist in array
int searchIdx = -1;
for (int i = 0; i < size; i++) {
// If element is found in array then save its index
// and terminate from loop.
if (arr[i] == toSearch) {
searchIdx = i;
break;
}
}
// If element is not found in array
if (searchIdx != -1) {
System.out.println(toSearch + " is found at position " + (searchIdx + 1));
} else {
System.out.println(toSearch + " is not found in the array");
}
scanner.close();
}
}
Problem 4: Write a java program to right rotate array by n position.
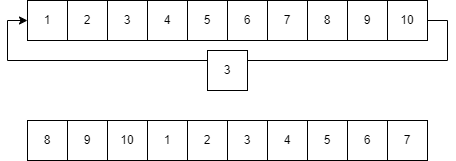
In the right rotation, each element of the array will be shifted to its right by one position and the last element of the array will be added to start of the list.
Note:
"n " can also be negative. Negative value of n means left rotation i.e. opposite of right rotation.
"n" can also be greater than the size of array.
Input
Size of array: 10
Elements of array: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Number of times to rotate: 3Output
8, 9, 10, 1, 2, 3, 4, 5, 6, 7Approach 1
Explanation/Steps
- Firstly, since the count to rotate the array can be greater than the size of array, so we need to take its modulus with the size of the array.
- Next, the count can be negative too, so we can left rotate or right rotate the array simply depending on that. But if you carefully notice the below diagram,
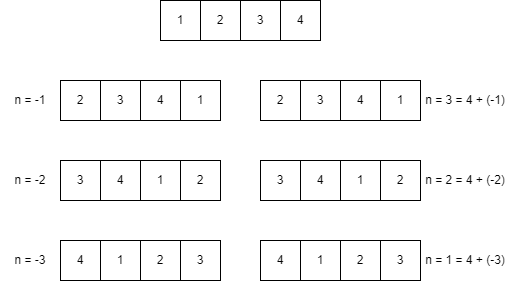
Count to rotate the array(in positive) = Count to rotate the array(in negative) + size of the arrayCount to rotate the array(in positive) = Count to rotate the array(in negative) + size of the array
- Now, we will be rotating the array n times one by one.
- For that, we need to store the value of first element in the array.
- Next, we will each element with the element to its right.
- And finally, at the last position, we will the value of first element that we has stored.
Solution
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// Input size of array
Scanner scanner = new Scanner(System.in);
System.out.println("Enter size of array: ");
int size = scanner.nextInt();
int[] arr = new int[size];
// Input elements of array
System.out.println("Enter elements in array: ");
for (int i = 0; i < size; i++) {
arr[i] = scanner.nextInt();
}
System.out.println("Enter number of times to left rotate: ");
int count = scanner.nextInt();
// Actual rotation
count = ((count % size) + size) % size;
// Print array before rotation
System.out.println("Array before rotation");
printArray(arr);
// Rotate array N times
for (int i = 1; i <= count; i++) {
rotateByOne(arr);
}
// Print array after rotation
System.out.println("Array after rotation");
printArray(arr);
scanner.close();
}
public static void rotateByOne(int[] arr) {
int size = arr.length;
// Store the last element of array
int last = arr[size - 1];
for (int j = 1; j <= size - 1; j++){
// Move each array element to its right
arr[size - j] = arr[size - 1 - j];
}
// Copies the last element of array to the first
arr[0]= last;
}
// Print the given array
public static void printArray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
Approach 2
Explanation/Steps
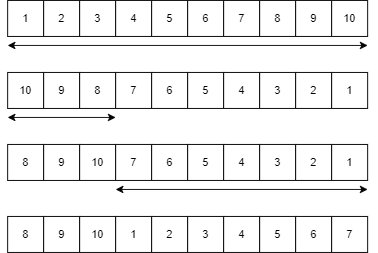
The above diagram clearly shows that reversing the array, then reversing the first count elements and finally reversing the elements after the count elements, eventually rotates the whole array count no of times.
I hope you remember how to reverse an array.
Solution
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
// Input size of array
Scanner scanner = new Scanner(System.in);
System.out.println("Enter size of array: ");
int size = scanner.nextInt();
int[] arr = new int[size];
// Input elements of array
System.out.println("Enter elements in array: ");
for (int i = 0; i < size; i++) {
arr[i] = scanner.nextInt();
}
System.out.println("Enter number of times to left rotate: ");
int count = scanner.nextInt();
// Actual rotation
count = ((count % size) + size) % size;
// Print array before rotation
System.out.println("Array before rotation");
printArray(arr);
// Rotate array N times
// Reversing the whole array
swap(arr, 0, size - 1);
// Reversing the first count elements
swap(arr, 0, count - 1);
// Reversing the elements after count elements
swap(arr, count, size - 1);
int i = 0, j = size - 1;
// Print array after rotation
System.out.println("Array after rotation");
printArray(arr);
scanner.close();
}
public static void swap(int[] arr, int start, int end){
while(start <= end){
int temp = arr[start];
arr[start] = arr[end];
arr[end] = temp;
start++;
end--;
}
}
// Print the given array
public static void printArray(int[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
}
}
Finally, we have reached the end of the practice questions on arrays.
Wohooo!
With this, I hope you now have a comprehensive understanding of arrays. Just keep practicing to strengthen them.